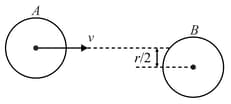
The diagram shows the velocity as a function of the time for an object with mass $10\mathrm{kg}$ being pushed along a frictionless surface by external force. At $t=3\mathrm{s}$, the force stops pushing and the object moves freely. It then collides head on and sticks to another object of mass $25\mathrm{kg}$:-

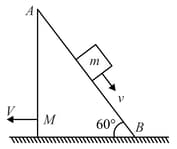
A particle of mass $m=0.1 \mathrm{kg}$ is released from rest from a point $A$ of a wedge of mass $M=2.4 \mathrm{kg}$ free to slide on a frictionless horizontal plane. The particle slides down the smooth face $AB$ of the wedge. When the velocity of the wedge is $0.2 \mathrm{m} {\mathrm{s}}^{-1}$ the velocity of the particle in $\mathrm{m} {\mathrm{s}}^{-1}$ relative to the wedge is:-

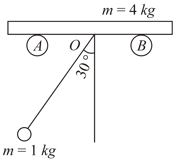
A ball of mass $1 \mathrm{kg}$ is suspended by an inextensible string $1 \mathrm{m}$ long attached to a point $O$ of a smooth horizontal bas resting on a fixed smooth supports $A$ and $B$. The ball is released from rest from the position when the string makes an angle of $30°$ with the vertical. The mass of the bar is $4 \mathrm{kg}$. The displacement in meters of the bar when the string makes the maximum angle on the other side of the vertical is:-

Find the distance between centre of gravity and centre of mass of a two particle system attached to the ends of a light rod. Each particle has same mass. Length of the rod is $R$, where $R$ is the radius of earth:-

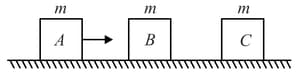
Three blocks $A,B$ and $C$ each of mass $\mathrm{m}$ are placed on a surface as shown in the digram. Blocks $B$ and $C$ are initially at rest. Block $A$ is moving to the right with speed $v$. It collides with block $B$ and sticks to it. The $A-B$ combination collides elastically with block $C$. Which of the following statement is (are) true about the velocity, of block $B$ and $C$.

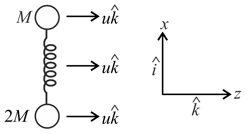
Two masses $A$ and $B$ of mass $M$ and $2M$ respectively are connected by a compressed ideal spring. The system is placed on a horizontal frictionless table and given a velocity $u\hat{k}$ in the $z$-direction as shown in the digram. The spring is then released. In the subsequent motion the line from $B$ to $A$ always points along the $\hat{i}$ unit vector. At some instant of time mass $B$ has a $x$-component of velocity as $v_x\hat{i}$. The velocity ${\overrightarrow{v}}_A$ of mass $A$ at that instant is:-

A disk $A$ of radius $r$ moving on perfectly smooth surface at a speed $v$ undergoes an elastic collision with an identical stationary disk $B$. Find the velocity of the disk $B$ after collision if the impact parameter is $\frac{r}{2}$ as shown in the figure:-