EASY
Earn 100
The distance between the points and is?
( Where above coordinates are in the polar coordinate system)
(a)
(b)
(c)
(d)
50% studentsanswered this correctly
Important Questions on Straight Lines
EASY
The equation of the graph shown here is:
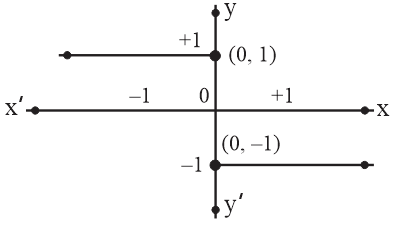
MEDIUM
Find the area of the triangle formed with the three straight lines represented by:
HARD
EASY
EASY
MEDIUM
MEDIUM
Find the ratio in which line divides the line segment joined by points and
MEDIUM
HARD
EASY
MEDIUM
MEDIUM
EASY
HARD
MEDIUM
Locus of the image of the point in the line is a
HARD
MEDIUM
EASY
MEDIUM
HARD

