MEDIUM
MHT-CET
IMPORTANT
Earn 100
The energy of a particle executing simple harmonic is given by , where is the displacement from mean position and is the velocity of the particle at then choose the incorrect statement.
(a)Amplitude of is .
(b)Maximum velocity of the particle during is .
(c)Time period of motion is .
(d)Displacement of the particle is proportional to the velocity of the particle.
50% studentsanswered this correctly

Important Questions on Oscillations
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
A block of mass is attached with two springs of spring constant is performing on a smooth horizontal surface. One of the spring is cut when the block is at the extreme position. Find the ratio of the amplitude of new and old
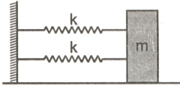
EASY
MHT-CET
IMPORTANT
A spring block system is put into SHM in two experiments. In the first, the block is pulled from the equilibrium position through a displacement and then released. In the second, it is pulled from the equilibrium position through a greater distance and then released. For both the experiments, which of the following is incorrect?
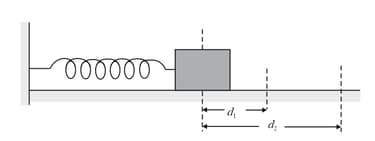
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
MEDIUM
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
