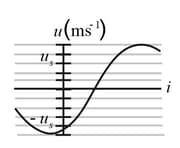
The figure shown below shows the transverse velocity $u$ versus time $t$ of the point on a string at $x=0,$ as a wave passes through. The scale on the vertical axis is set by $u_x=12 \mathrm{m} {\mathrm{s}}^{-1}$. The wave has generic form $y(x,t)=y_{m}sin(kx-\omega t+\varphi ).$ What then is $\varphi ?$ (A calculator does not always give the proper inverse trigonometric function, so check your answer by substituting it and an assumed value of $\omega$ into $y(x, t)$ and then plotting the function.)

These two waves travel along the same string:
$y_1(x,t)=(4.00 \mathrm{mm})sin(2\pi x-650\pi t)$
$y_2(x,t)=(6.20 \mathrm{mm})sin(2\pi x-650\pi t+0.60\pi \mathrm{rad})$.

What are

(a) the amplitude

(b) the phase angle (relative to wave $1$) of the resultant wave?

(c) If a third wave of amplitude $5.00 \mathrm{mm}$ is also to be sent along the string in the same direction as the first two waves, what should be its phase angle in order to maximize the amplitude of the new resultant wave?

A standing wave pattern on a string is described by $y(x,t)=0.040\left(sin4\pi x\right)\left(cos40\pi t\right)$, where $\mathrm{x}$ and $\mathrm{y}$ are in metres and $\mathrm{t}$ is in seconds.
For $x\ge 0,$ what is the location of the node with the

$\left(a\right)$ smallest

$\left(b\right)$ second smallest

$\left(c\right)$ third smallest value of $x?$
$\left(d\right)$ What is the period of the oscillatory motion of any (non-node) point? 

What are the

$\left(e\right)$ speed

$\left(f\right)$ amplitude of the two traveling waves that interfere to produce this wave?
For $t\ge 0,$ what are the

$\left(g\right)$ first 

$\left(\mathrm{h}\right)$ second, and
$\left(i\right)$ third time that all points on the string have zero transverse velocity?

A sinusoidal wave is sent along a string with a linear density of $\mu =5.0 \mathrm{g} {\mathrm{m}}^{-1}$. As it travels, the kinetic energies of the mass elements along the string vary. The figure shown below gives the rate $\frac{\mathrm{dK}}{dt}$ at which kinetic energy passes through the string elements at a particular instant, plotted as a function of distance $x$ along the string. The figure shown below is similar except that it gives the rate at which kinetic energy passes through a particular mass element (at a particular location), plotted as a function of time $\mathrm{t}$. For both figures, the scale on the vertical (rate) axis is set by $R_{\mathrm{s}}=10 \mathrm{W}$. What is the amplitude of the wave?

The equation of a transverse wave travelling along a very long string is $y=3.0sin(0.020\pi x-4.0\pi t),$ where $x$ and $y$ are expressed in centimetres, and $t$ is in seconds. Determine

(a) the amplitude

(b) the wavelength

(c) the frequency

(d) the speed

(e) the direction of propagation of the wave

(f) the maximum transverse speed of a particle in the string.

(g) What is the transverse displacement at $x=3.5 \mathrm{cm}$ when $t=0.26 \mathrm{s}?$

What are

(a) the lowest frequency

(b) the second lowest frequency

(c) the third lowest frequency

for standing waves on a wire that is $10.0 \mathrm{m}$ long, has a mass of $100 \mathrm{g}$, and is stretched under a tension of $275 \mathrm{N}$?

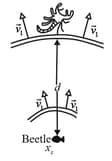
A sand scorpion can detect the motion of a nearby beetle (its prey) by the waves the motion sends along the sand surface (in the figure shown below). The waves are of two types, transverse waves travelling at $v_{\mathrm{t}}=50 \mathrm{m} {\mathrm{s}}^{-1}$ and longitudinal waves traveling at $v_{\mathrm{l}}=150 \mathrm{m} {\mathrm{s}}^{-1}$. If a sudden motion sends out such waves, a scorpion can tell the distance of the beetle from the difference $∆t$ in the arrival times of the waves at its leg nearest the beetle. What is the time difference if the distance to the beetle is $37.5 \mathrm{cm}?$