MEDIUM
JEE Main
IMPORTANT
Earn 100
The figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to the initial horizontal velocity component, keeping the highest first.
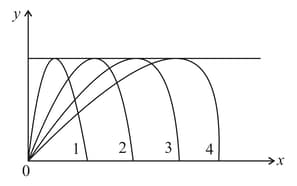

(a)
(b)
(c)
(d)
50% studentsanswered this correctly

Important Questions on Motion in Two Dimensions
EASY
JEE Main
IMPORTANT
Four bodies and are projected with equal velocities, having angles of projection and with the horizontal respectively. The body having the shortest range is
MEDIUM
JEE Main
IMPORTANT
The path of a projectile in the absence of air drag is shown in the figure by a dotted line. If the air resistance is not ignored, then, which one of the paths shown in the figure, is appropriate for the projectile?
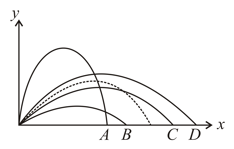
EASY
JEE Main
IMPORTANT
A stone projected with a velocity at an angle with the horizontal, reaches a maximum height When it is projected with velocity at an angle with the horizontal, it reaches maximum height . If is the range in both the cases, the correct relation is
MEDIUM
JEE Main
IMPORTANT
An object is projected with a velocity of making an angle of with horizontal. The equation for the trajectory is, where is height, is horizontal distance and and are constants. The ratio is
MEDIUM
JEE Main
IMPORTANT
For a given velocity, a projectile has the same range for two angles of projection. If and are the times of flight in the two cases, then
MEDIUM
JEE Main
IMPORTANT
A stone is projected from the ground with a velocity at an angle of . It crosses a wall after . How far beyond the wall will the stone strike the ground ?
EASY
JEE Main
IMPORTANT
A particle is projected with a velocity such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is ( is the acceleration due to gravity.)
EASY
JEE Main
IMPORTANT
A man standing on the roof of a house of height , throws one particle vertically downwards and another particle horizontally with the same velocity . The ratio of their velocities, when they reach the Earth’s surface, will be
