The function, $x=A{\sin }^2\omega t+B{\cos }^2\omega t+C\mathrm{sin\omega }t\mathrm{cos\omega }t$ represents S.H.M.,

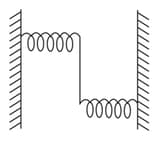
A uniform rod of length $L$ and mass $M$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $k$. The springs are fixed to rigid supports as shown in the figure and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $\mathrm{\theta }$ in one direction and released. The frequency of oscillation is,

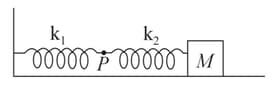
The mass $M$ shown in the figure oscillates in simple harmonic motion with amplitude $A$. The amplitude of the point $P$ is,

A metal rod of length $L$ and mass $m$ is pivoted at one end. A thin disk of mass $M$ and radius $R$ ($<L$) is attached at its centre to the free end of the rod. Consider two ways the disc is attached:

(Case $A$): The disc is not free to rotate about its centre and

(Case $B$): the disc is free to rotate about its centre.

The rod- disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true?

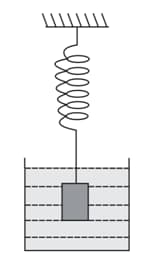
Consider the spring-mass system with the mass submerged in water as shown in the figure. The phase space diagram for one cycle of this system is,

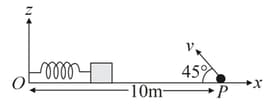
A small block is connected to one end of a massless spring of un-stretched length $4.9 \mathrm{m}$. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by $0.2 \mathrm{m}$ and released from rest at $t=0$. It then executes simple harmonic motion with angular frequency, $\mathrm{\omega }=\frac{\mathrm{\pi }}{3} \mathrm{rad} {\mathrm{s}}^{-1}$. Simultaneously, at $t=0$, a small pebble is projected with speed $v$ from point $P$ at an angle of $45°$ as shown in the figure. The point $P$ is at a horizontal distance of $10 \mathrm{cm}$ from $O$. If the pebble hits the block at $t=1 \mathrm{s}$, the value of $v$ is (take, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$),

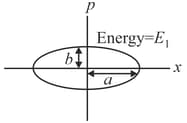
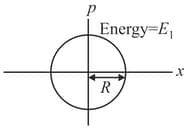
Two independent harmonic oscillators of equal masses oscillate about the origin with angular frequencies ${\mathrm{\omega }}_1$ and ${\mathrm{\omega }}_2$ and have total energies $E_1$ and $E_2$, respectively. The variations of their momenta $p$ with positions $x$ are shown in figures. If $\frac{a}{b}=n^2$ and $\frac{a}{R}=n$, then the correct equation(s) is (are),