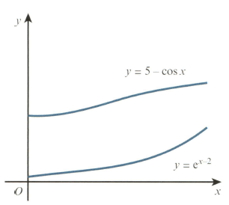
The functions and are defined, for by and
The diagram shows the graph of and the graph of
The gradients of the curves are equal both when and when
Given that verify by calculation that is correct to decimal places.
The diagram shows the graph of and the graph of
The gradients of the curves are equal both when and when


Important Questions on Numerical Solutions of Equations
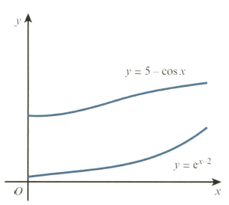
The functions and are defined, for by and
The diagram shows the graph of and the graph of
The gradients of the curves are equal both when and when
Show that satisfies the equation
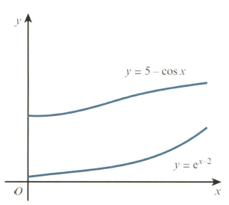
The functions and are defined, for by and
The diagram shows the graph of and the graph of
The gradients of the curves are equal both when and when
Given also that use the iterative formula to calculate correct to decimal places, showing the result of each iteration to decimal places.
The equation has a root that lies between and
Show that is also a root of the equation
The equation has a root that lies between and
Using the iterative formula find the value of giving your answer correct to decimal places.
