The gravitational potential energy is maximum at

A spherically symmetric gravitational system of particles has mass density $\rho =\left\{\begin{array}{l}{\rho }_0\text{ for }r\le R\\ 0\text{ for }r>R\end{array}\right.$ where, ${\rho }_0$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed $v$ as a function of distance $r(0<r<\infty )$ from the centre of the system is represented by

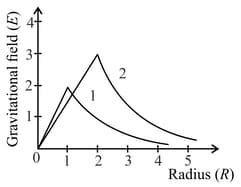
Consider two solid spheres of radii $R_1=1 \mathrm{m}$,$R_2=2 \mathrm{m}$ and masses $M_1$ and $M_2,$ respectively. The gravitational field due to sphere $\left(1\right)$ and $\left(2\right)$ are shown. The value of $\frac{M_1}{M_2}$ is:

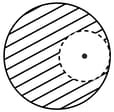
From a solid sphere of mass $M$ and radius $R\text{,}$ a spherical portion of radius $\left(\frac{R}{2}\right)$ is removed as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty ,$ the potential at the centre of the cavity thus formed is ($G=$gravitational constant)

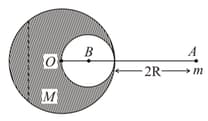
A solid sphere of radius $R$ gravitationally attracts a particle placed at $3R$ from its centre with a force $F_1.$ Now a spherical cavity of radius $\left(\frac{R}{2}\right)$ is made in the sphere (as shown in figure) and the force becomes $F_2$. The value of $F_1:F_2$ is:

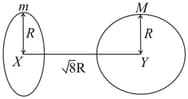
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If $\sqrt{8}R$ is the distance between the centres of a ring (of mass $m$) and a sphere (mass $M$) where both have equal radius $R$

Inside a uniform spherical shell :

(a) The gravitational field is zero.

(b) The gravitational potential is zero.

(c) The gravitational field is the same everywhere.

(d) The gravitation potential is the same everywhere.

(e) All the above.

Choose the most appropriate answer from the options given below: