The height at which the acceleration due to gravity becomes $g/9$ (where $g=$ the acceleration due to gravity on the surface of earth) in terms of $\mathrm{R}$, the radius of the earth is

What is the minimum energy required to launch a satellite of mass $\mathrm{m}$ from the surface of a planet of mass  $\mathrm{M}$ and radius $\mathrm{R}$ in a circular orbit at an altitude of $2\mathrm{R}?$

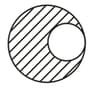
From a solid sphere of mass $M$ and radius $R$, a spherical portion of radius $\frac{R}{2}$ is removed, as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty$, the potential at the centre of the cavity thus formed is:($G=$ gravitational constant)