The household supply of electricity is at $220 \mathrm{V}$ (RMS value) and $50 \mathrm{Hz}$. Find the peak voltage and the least possible time in which the voltage can change from the RMS value to zero.

(i) A current that changes its direction periodically is called alternating current ($\mathrm{AC}$). If a current maintains its direction constant it is called direct current ($\mathrm{DC}$).

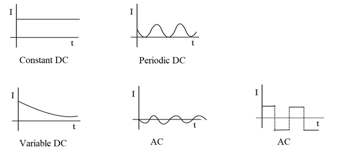
(ii) Average value: $I_{\mathrm{avg}}=\frac{{\int }_0^{T}I\mathrm{d}t}{{\int }_0^T\mathrm{d}t}=\frac{1}{T}{\int }_0^{\tau }I\mathrm{d}t$

(iii) RMS value: $I_{\mathrm{rms}}=\sqrt{\frac{{\int }_0^T{I}^2\mathrm{d}t}{{\int }_0^T\mathrm{d}t}}$

(iv) For a sinusoidal voltage $V=V_0\sin \omega t: V_{\mathrm{avg}}=\frac{2 V_0}{\pi } \& V_{\mathrm{rms}}=\frac{V_0}{\sqrt{2}}$, where $V_0$ is the peak voltage, $\omega$ is the angular frequency of the source.

(v) For a sinusoidal current $I=I_0\sin \left(\omega t+\varphi \right): l_{\mathrm{avg}}=\frac{2I_0}{\pi } \& I_{\mathrm{rms}}=\frac{I_0}{\sqrt{2}}$, where $I_0$ is the peak current.

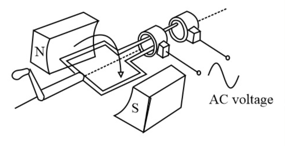
2. AC generator:

An $\mathrm{AC}$ generator is an electric generator that converts mechanical energy into electrical energy in form of an alternative emf or alternating current. $\mathrm{AC}$ generators work on the principle of electromagnetic induction.

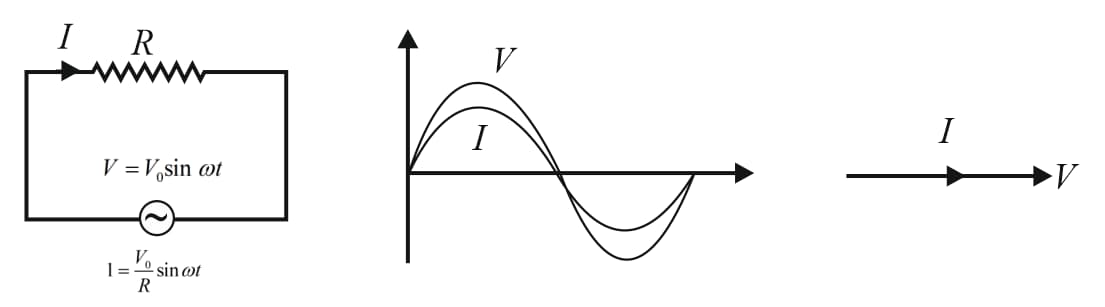
3. AC circuit:

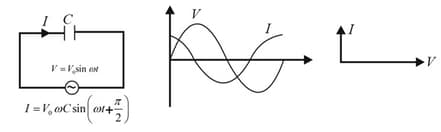(i) In a pure resistor, current and voltage are in phase.

(ii) In a pure capacitor, the current leads the voltage by $90°$

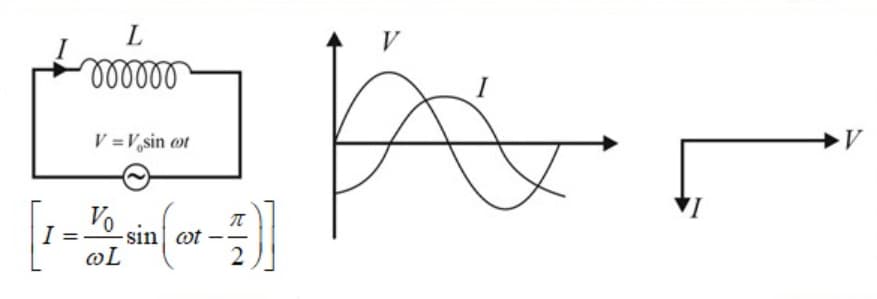
(iii) In a pure inductor, the current lags the voltage by $90°$

4. Reactance and Impedance:

(i) ωL is called inductive reactance and is denoted by XL

(ii) 1ωC is called capacitive reactance and is denoted by XC

5. Series LCR Circuit:

Consider a series $\mathrm{LCR}$ series circuit with resistance $R$, inductive reactance $X_{\mathrm{L}}$, and capacitive reactance $X_{\mathrm{C}}$.
(i) Impedance, $Z=\sqrt{R^2+{\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)}^2}$

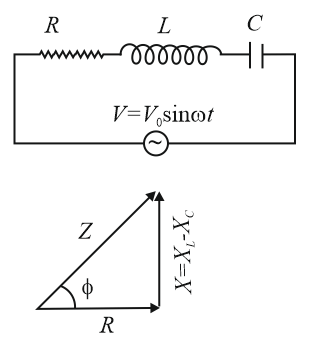
(ii) Applied voltage in terms of voltages across the components, V=VR2+VL-VC2

6. Power in AC Circuits and Wattless current:

(i) Average power consumed in a cycle $=\frac{{\int }_0^{\frac{2\pi }{\omega }}P\mathrm{d}t}{\left(\frac{2\pi }{\omega }\right)}=\frac{1}{2}{V}_{\mathrm{m}}{I}_{\mathrm{m}}\cos \phi$

(ii) $P_{\mathrm{avg}}=\frac{V_{\mathrm{m}}}{\sqrt{2}}\frac{I_{\mathrm{m}}}{\sqrt{2}}\cos \phi =V_{\mathrm{rms}} I_{\mathrm{rms}\mathrm{ }}\cos \phi =\frac{V_{\mathrm{rms}}^2}{R}$, here $\cos \phi$ is called a power factor.

(iii) The current in $\mathrm{AC}$ circuit is said to be wattless current when the average power consumed in such circuit corresponding to zero such current is also called idle current.

7. Wattless current:

In an $\mathrm{AC}$ circuit, if the average power consumed is zero, then the current is called a wattless current. Its formula is $I_{\mathrm{rms}}\sin \varphi$, where ϕ is the phase difference between current and voltage applied.

8. Resonance:

(i) At resonance: XL=Xc⇒Z=R,V=VR

(ii) Resonant frequency is fr=12πLC, where L is the inductance, and C is capacitance.

(iii) Nature of the circuit is resistive.

(iv) Current in the circuit is maximum, i.e., i0=V0R

(v) Power consumed at resonance is $P_{\mathrm{avg}}=\frac{V_{\mathrm{rms}}^2}{R}$

9. Bandwidth:

The bandwidth of $\mathrm{RLC}$ series circuit of resistance $R$, inductance $L$, and Capacitance $C$ is
BW=RL

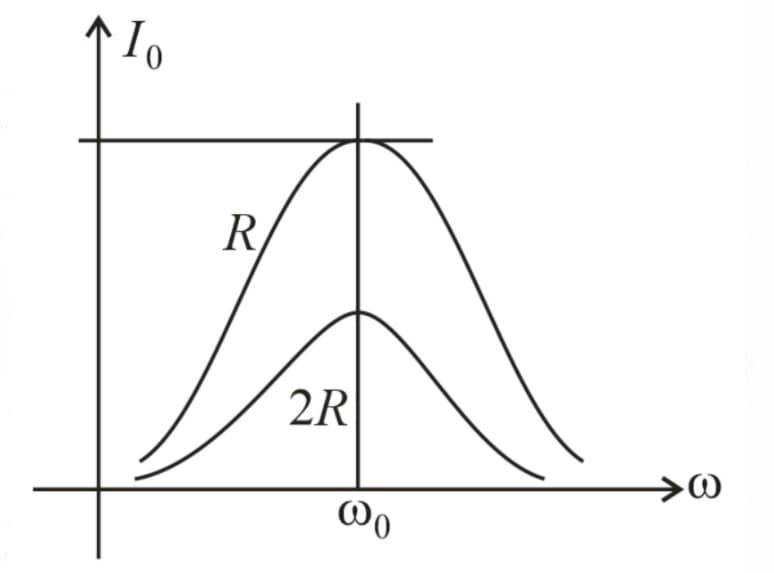
As the resistance increases, peak current decreases, and the bandwidth increases.

10. Quality factor:

(i) $Q$ factor (also known as a Quality factor or $Q$-factor) is defined as a dimensionless parameter that describes the underdamped condition of an oscillator or resonator.
(ii) The quality factor of series RLC circuit of resistance $R$, inductance $L$, and Capacitance $C$ is

$Q=\frac{f_r}{BW}=\frac{X_L \text{or} X_C}{R}=\frac{1}{R}\sqrt{\frac{L}{C}}$

11. LC oscillations:

(i) Charge at time $t$ is $q=q_0\sin \left(\omega t+\theta \right)$, and current at time $t$ is $I=I_0\cos \left(\omega t+\theta \right)$, where maximum current $I_0=q_0\omega$.
$q_0$ is the maximum charge on the capacitor, and $\omega$ is the angular frequency with which the current ocillates.

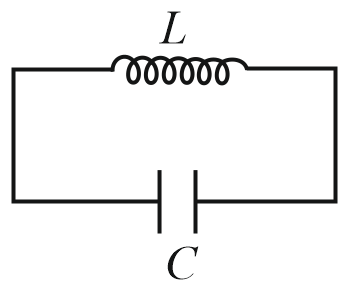
(ii) Energy $=\frac{1}{2}L{i}^2+\frac{q^2}{2C}=\frac{q_0^2}{2C}=\frac{1}{2}L{i}_0^2=\mathrm{constant}$, where $L$ is inductance, and $C$ is the capacitance.

(iii) Comparison of $\mathrm{LC}$ oscillations with $\mathrm{SHM}$ of spring:  $q\to x, I\to v, L\to m, C\to \frac{1}{K}$

12. Comparison of damped mechanical & electrical systems:

(i) Series $\mathrm{LCR}$ circuit:
Consider a resistance $R$, inductnace $L$, and capacitance $C$ are connected in series. Let $q$ be the charge on the capacitor at time $t$. Then,

$\frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=\frac{V_0}{L}\cos \omega t$

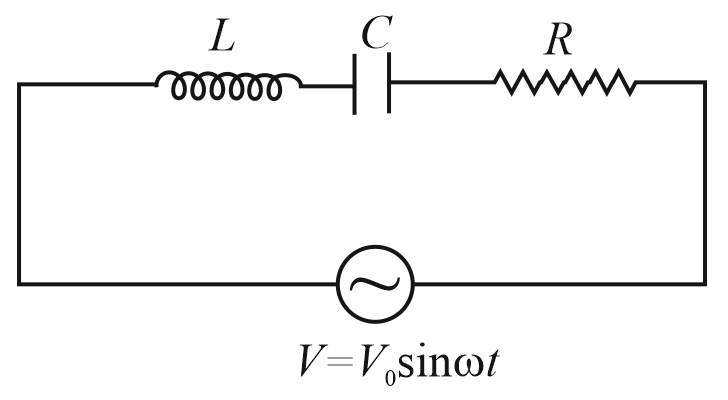
compare with the mechanical damped system equation,

$\frac{d^{2}x}{d{t}^2}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=\frac{F_0}{m}\cos \omega t$, where b=damping coefficient.

(ii) Parallel $\mathrm{LCR}$ circuit:

(a) Consider a resistance $R$, inductnace $L$, and capacitance $C$ are connected in parallel. Let $q$ be the charge on the capacitor at time $t$. Then,

$I=I_L+I_C+I_R=\frac{\varphi }{L}+\frac{\mathrm{d}}{\mathrm{d}t}C\left(\frac{d\varphi }{dt}\right)+\frac{1}{R}\frac{\mathrm{d}\varphi }{\mathrm{d}t}\Rightarrow \frac{{\mathrm{d}}^2\varphi }{\mathrm{d}{t}^2}+\frac{1}{RC}\frac{\mathrm{d}\varphi }{\mathrm{d}t}+\frac{1}{LC}\varphi =\frac{V_0}{Z}\sin \omega t$

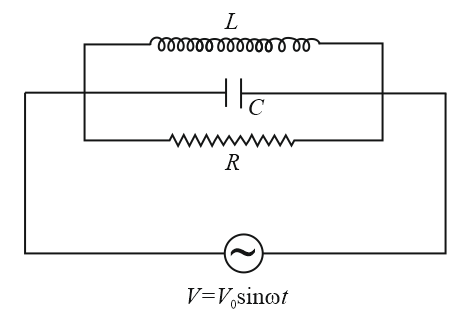
(b) Displacement $\left(x\right)$ $⟹$Flux linkage $\left(\varphi \right)$

(c) Velocity $\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)$$⟹$Voltage $\left(\frac{\mathrm{d}\varphi }{\mathrm{d}t}\right)$

(d) Mass $\left(m\right)$ ⟹Capacitance $\left(C\right)$

(e) Spring constant $\left(k\right)$ ⟹Reciprocal Inductance 1L

(f) Damping coefficient $\left(b\right)$ ⟹Reciprocal resistance $\left(\frac{1}{R}\right)$; Driving force $\left(F\right)$ ⟹Current $\left(i\right)$