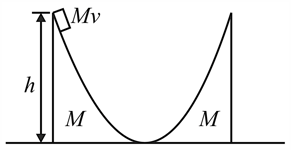
The inclined surfaces of two movable wedges of the same mass are smoothly conjugated with the horizontal plane (Fig.). A washer of mass slides down the left wedge from a height .
To what maximum height will the washer rise along the right wedge? Friction should be neglected.


Important Questions on Mechanics
1.55. A symmetric block of mass $m_{1}$ with a notch of hemispherical shape of radius $r$
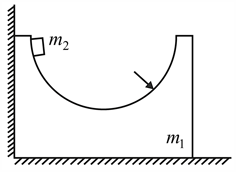
rests on a smooth horizontal surface near the wall (Fig.). A small washer of mass slides without friction from the initial position.
Find the maximum velocity of the block.
Determine the time dependences of the displacement of the washer and of its velocity relative to the table, starting from the instant and assuming
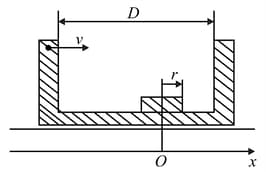
that all the impacts of the washer against the box are perfectly elastic. Plot the graphs and The friction between the box and the washer should be neglected.
A ring of mass connecting freely two identical thin hoops of mass each starts sliding down. The hoops move apart over a rough horizontal surface.
Determine the acceleration of the ring at the initial instant if
(Fig.), neglecting the friction between the ring and the hoops.
A flexible pipe of length $l$ connects two points and in space with an altitude difference (Fig.). A rope passed through the pipe is fixed at point .
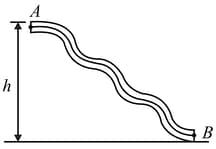
Determine the initial acceleration of the rope at the instant when it is released, neglecting the friction between the rope and the pipe walls.
A smooth washer impinges at a velocity on a group of three smooth identical blocks resting on a smooth horizontal surface as shown in Fig. The mass of each block is equal to the mass of the washer. The diameter of the washer and its height are equal to the edge of the block.
Determine the velocities of all the bodies after the impact.
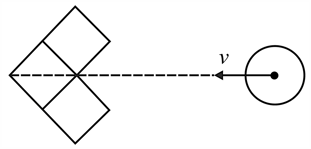
Determine the final velocity of the body formed as a result of all collisions, assuming that the collisions are perfectly inelastic.
Three small bodies with the mass ratio (the mass of the lightest body is ) are kept at three different points on the inner surface of a smooth hemispherical cup of radius . The cup is fixed at its lowest point on a horizontal surface. At a certain instant, the bodies are released.
Determine the maximum amount of heat that can be liberated in such a system. At what initial arrangement of the bodies will the amount of liberated heat be maximum? Assume that collisions are perfectly inelastic.
