The length, breadth and height of a room are in the ratio $3:2:1$. If the breadth and height are halved while the length is doubled, then the total area of the four walls of the room will :

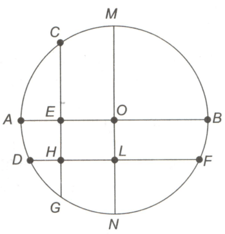
In the following figure, the diameter of the circle is $3 \mathrm{cm}. \mathrm{AB}$ and $\mathrm{MN}$ are two diameters such that $\mathrm{MN}$ is perpendicular to $\mathrm{AB}.$ In addition, $\mathrm{CG}$ is perpendicular to $\mathrm{AB}$ such that $\mathrm{AE}: \mathrm{EB}=1: 2,$ and $\mathrm{DF}$ is perpendicular to $\mathrm{MN}$ such that $\mathrm{NL}: \mathrm{LM}=1: 2.$ The length of $\mathrm{DH}$ in $\mathrm{cm}$ is

Consider the triangle $ABC$ shown in the following figure where $BC=12 \mathrm{cm}, DB=9 \mathrm{cm}, CD=6 \mathrm{cm}$ and $\angle BCD=\angle BAC.$

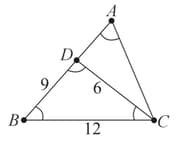
What is the ratio of the perimeter of $\mathit{∆}ADC$ to that of $\Delta BDC?$

A jogging park has two identical circular tracks touching each other, and a rectangular track enclosing the two circles. The edges of the rectangles are tangential to the circles. Two friends, $\mathrm{A}$ and $\mathrm{B},$ start jogging simultaneously from the point where one of the circular tracks touches the smaller side of the rectangular track. $\mathrm{A}$ jogs along the rectangular track, while $\mathrm{B}$ jogs along the two circular tracks in a figure of eight. Approximately, how much faster than $\mathrm{A}$ does $\mathrm{B}$ have to run, so that they take the same time to return to their starting point ?