Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 35

HARD

Mathematics

IMPORTANT

Earn 100

The maximum value of $P = x + 3 y$ , such that $2 x + y \leq 20, x + 2 y \leq 20, x \geq 0, y \geq 0$ is

50% studentsanswered this correctly

Important Questions on Linear Programming

MEDIUM

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 36

Consider $z = - 2 x - 3 y$ subject to $\frac{x}{2} + \frac{y}{3} \leq 1, \frac{x}{3} + \frac{y}{2} \leq 1, x, y \geq 0$ . The maximum value of $z$ is

HARD

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 37

The solution region satisfied by the inequalities

x + y \leq 5, x \leq 4, y \leq 4, x \geq 0, y \geq 0, 5 x + y \geq 5, x + 6 y \geq 6

is bounded by

HARD

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 38

Corner points of the feasible region determined by the system of linear constraints are

(0, 3), (1, 1)

and

(3, 0) .

Let

Z = p x + q y,

where

p, q > 0 .

Condition on

p

and

q

so that the minimum of

Z

occurs at

(3, 0)

and

(1, 1)

is

MEDIUM

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 39

The corner points of the feasible region determined by the system of linear constraints are

(0, 10), (5, 5) (15, 15), (0, 20) .

Let

Z = p x + q y,

where

p, q > 0 .

Condition on

p

and

q

so that the maximum of

Z

occurs at both the points

(15, 15)

and

(0, 20)

is

MEDIUM

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 40

The region represented by the inequalities

x \geq 6, y \geq 2, 2 x + y \leq 10, x \geq 0, y \geq 0

is

MEDIUM

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 41

Let

Z = 7 x + y

subjected to

5 x + y \geq 5, x + y \geq 3, x \geq 0, y \geq 0 .

The minimum value of

Z

occurs at

HARD

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 42

The solution set of the following system of inequations

x + 2 y \leq 3, 3 x + 4 y \geq 12, x \geq 0, y \geq 1,

is

MEDIUM

Mathematics

IMPORTANT

Mathematics Crash Course BITSAT>Chapter 19 - Linear Programming>Exercise 1>Q 43

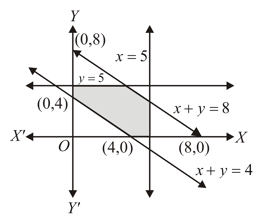
Linear inequalities for which the shaded region of the given figure is the solution set, are

Question Image