The measure of each interior angle of a regular polygon is 150 degrees . Therefore, the number of sides of the polygon is .

The number of sides of two regular polygons is in the ratio $5 : 4$. The difference between their interior angles is $9°$. Consider the following statements:

$1)$ One of them is a pentagon and the other is a rectangle.

$2)$ One of them is a decagon and the other is an octagon.

$3)$ The sum of their exterior angles is $720°$.

Which of the above statements is/are correct?

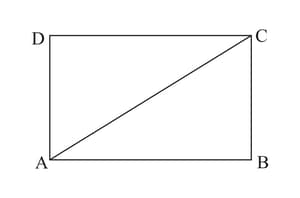
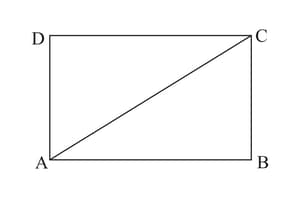
Perimeter of the rectangle in the figure is $36 centimetres$. $AC=\sqrt{164} centimetres.$ Find length of $AB$.

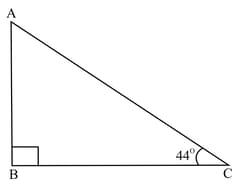
In triangle $ABC, \angle A=\angle B=30°, AC=4 centimetres$. What is the length of $BC$?

Given that the angles of a polygon are all equal and each angle is a right angle.

Statement-$1$: The polygon has exactly four sides.

Statement-$2$: The sum of the angles of a polygon having $n$ sides is $(3n-8)$ right angles.

Which one of the following is correct in respect of the above statements?

Perimeter of the rectangle in the figure is $36 centimetres$. $AC=\sqrt{164} centimetres.$ What is $AB+BC$? 

In the figure, $\angle B=90°, \angle C=44°$

What is the measure of $\angle A$?

All congruent polygon are _____.

If the measure of each exterior angle of a regular polygon is ${\left(51\frac{3}{7}\right)}^{\circ }$, then the ratio of the number of its diagonal to the number of its side is:

If the interior angle of a regularpolygon is $108°$, then it is a-

1. Octagon

2. Hexagon

3. Pentagon

4. Tetragon 

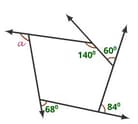
In the figure below, the measure of ∠$ \text{a}$=_____$ \text{°}$.