A thin uniform square plate, with side l and mass M , can rotate freely about a stationary vertical axis, coinciding with one of its sides. A small ball of mass m , flying with velocity v → , at right angles to the plate, strikes elastically at the centre of it. Find: ( a ) the velocity of the ball v ' → after the impact; ( b ) the horizontal component of the resultant force, which the axis will exert on the plate after the impact.

( a ) Since no external torque is acting on the system (but there is an external force which is hinge-force by axis), the angular momentum is conserved about the axis of rotation. Also, there are no forces which are non-conservative in nature. Thus, we can also conserve mechanical energy. 1 2 m v 2 = 1 2 m v ' 2 + 1 2 M l 2 3 ω 2 (By conservation of kinetic energy) And m v l 2 = m v ' l 2 + M l 2 3 ω (By conservation of angular momentum) By solving the two simultaneous equations, we get, v ' = 3 m - 4 M 3 m + 4 M v and ω = 4 v l ( 1 + 4 m 3 M ) Since v ' → ↑ ↑ v → , in vector format, v ' → = 3 m - 4 M 3 m + 4 M v → ( b ) Here, the hinge-force gives the necessary centripetal force to the centre of mass of the rod. Therefore, we can write, F n = m w c n = M ω 2 l 2 = 8 M v 2 l ( 1 + 4 M 3 m ) 2

HARD

JEE Main

IMPORTANT

Earn 100

The midpoint of a thin uniform rod $A B$ , of mass $m$ and length $l$ , is rigidly fixed to a rotation axle $O O^{'}$ , as shown in the figure. The rod is set into rotation with a constant angular velocity $ω$ . Find the resultant moment of the centrifugal forces of inertia, relative to the point $C$ , in the reference frame fixed to the axle $O O^{'}$ and to the rod.

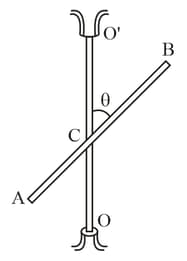
Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.270.

A conical pendulum, a thin uniform rod of length

l

and mass

m

, rotates uniformly about a vertical axis, with angular velocity

ω

( the upper end of the rod is hinged

)

. Find the angle

θ

between the rod and the vertical.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.271.

A uniform cube, with edge

a

, rests on a horizontal plane, whose friction coefficient equals

k

. The cube is set in motion with an initial velocity, travels some distance over the plane and comes to a stand-still. Explain the disappearance of the angular momentum of the cube, relative to the axis lying in the plane, at right angles to the cube's motion direction. Find the distance between the resultants of gravitational forces and the reaction forces exerted by the supporting plane.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.272.

A smooth uniform rod

A B

, of mass

M

and length

l

, rotates freely with an angular velocity

ω_{0}

, in a horizontal plane, about a stationary vertical axis passing through its end

A

. A small sleeve of mass

m

starts sliding along the rod from the point

A

. Find the velocity

v'

of the sleeve, relative to the rod, at the moment it reaches its other end

B

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.273.

A uniform rod of mass

m = 5.0 kg

and length

l = 90 cm

, rests on a smooth horizontal surface. One of the ends of the rod is struck with an impulse

J = 3.0 N s

, in the horizontal direction, perpendicular to the rod. As a result, the rod obtains the momentum

p = 3.0 N s

. Find the force that one half of the rod will apply on the other, in the process of motion.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.274.

A thin uniform square plate, with side

l

and mass

M

, can rotate freely about a stationary vertical axis, coinciding with one of its sides. A small ball of mass

m

, flying with velocity

\vec{v}

, at right angles to the plate, strikes elastically at the centre of it. Find:

(a)

the velocity of the ball

\vec{v^{'}}

after the impact;

(b)

the horizontal component of the resultant force, which the axis will exert on the plate after the impact.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.275.

A vertically oriented uniform rod, of mass

M

and length

l

, can rotate about its upper end. A horizontally flying bullet, of mass

m

, strikes the lower end of the rod and gets stuck on it; as a result, the rod swings through an angle

α

. Assuming that

m ≪ M,

find

(a)

the velocity of the flying bullet

(b)

the momentum increment in the system "bullet-rod" during the impact; what causes the change of that momentum

(c)

at what distance

x

, from the upper end of the rod, the bullet must strike, for the momentum of the system "bullet-rod" to remain constant during the impact.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.276.

A horizontally oriented uniform disc, of mass

M

and radius

R

, rotates freely about a stationary vertical axis, passing through its centre. The disc has a radial guide, along which can slide, without friction, a small body of mass

m

. A light thread, running down through the hollow axle of the disc, is tied to the body. Initially, the body was located at the edge of the disc and the whole system was rotated with an angular velocity

ω_{0}

. Then, by means of a force

F

applied to the lower end of the thread, the body was slowly pulled to the rotation axis. Find:

(a)

the angular velocity of the system in its final state;

(b)

the work performed by the force

F

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 1 - PHYSICAL FUNDAMENTALS OF MECHANICS>DYNAMIC OF A SOLID BODY>Q 1.277.

A man of mass

m_{1}

stands on the edge of a horizontal uniform disc of mass

m_{2}

and radius

R

, which is capable of rotating freely about a stationary vertical axis passing through its centre. At a certain moment, the man starts moving along the edge of the disc; he shifts over an angle

φ'

, relative to the disc, and then stops. In the process of motion, the velocity of the man varies with time as

v' (t)

. Assuming the dimensions of the man to be negligible, find:

(a)

the angle through which the disc had turned by the moment the man stopped;

(b)

the force moment (relative to the rotation axis) which the man applied on the disc, in the process of motion.

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS

Learn and Prepare for any exam you want !