The minimum force required to start pushing a body up a rough inclined plane (frictional coefficient $\mu$) is $F_1$ while the minimum force needed to prevent it from sliding down is $F_2$. If the inclined plane makes an angle $\text{θ}$ from the horizontal such that, $\tan \text{θ}$$=2\mu$, then, the ratio $\frac{F_1}{F_2}$ is 

What is the maximum value of force $F$ such that, the block, shown in the arrangement, does not move?

The system shown in the figure is in equilibrium. The maximum value of $W,$ so that, the maximum value of static frictional force on $100 \mathrm{kg}$ body is $450 \mathrm{N}$, will be 

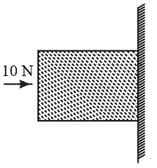
A horizontal force of $10 \mathrm{N}$ is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is $0.2$. The weight of the block is

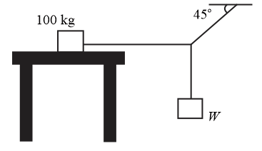
Two masses $A$ and $B$ of $10 \mathrm{kg}$, respectively, are connected with a string passing over a frictionless pulley fixed at the corner of a table, as shown in the figure. The coefficient of static friction of $A$ with the table is $0.2$. The minimum mass of $C$, that may be placed on $A$, to prevent it from moving, is

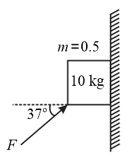
A force $F$ pushes a block weighing $10 \mathrm{kg}$ against a vertical wall, as shown in the figure. The coefficient of friction between the block and the wall is $0.5.$ The minimum value of $F$, to start the upward motion of block, is $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$

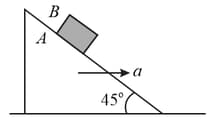
If the coefficient of friction between $A$ and $B$ is $\mu$, the maximum horizontal acceleration of the wedge $A$, for which $B$ will remain at rest with respect to the wedge, is

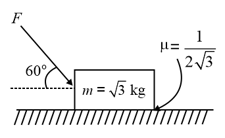
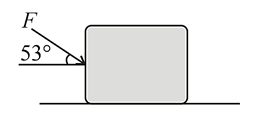
A block of mass $20 \mathrm{kg}$ is acted upon by a force $F=30 \mathrm{N}$, at an angle $53°$ with the horizontal, in the downward direction, as shown. The coefficient of friction between the block and the horizontal surface is $0.2$. The frictional force acting on the block by the ground is $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$ 

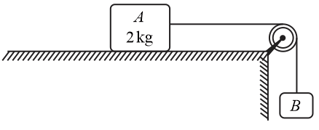
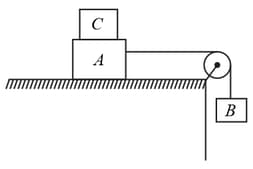
The coefficient of static friction ${\mu }_{\mathrm{s}}$ between block $A$ of mass $2 \mathrm{kg}$ and the table, as shown in the figure, is $0.2.$ What would be the maximum mass of block $B$, so that the two blocks do not move? (The string and the pulley are assumed to be smooth and massless) $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$