The nucleus of a hydrogen atom carries a charge of $+1.60 \times 10^{-19} \mathrm{C}$. Its electron is at a distance of $1.05 \times 10^{-10} \mathrm{~m}$ from the nucleus. Calculate the ionisation potential of hydrogen. (Hint: This is equal to the work per unit charge needed to remove the electron to infinity.)

Two charged conducting spheres, each of radius $1.0 \mathrm{~cm}$, are placed with their centres $10 \mathrm{~cm}$ apart, as shown.

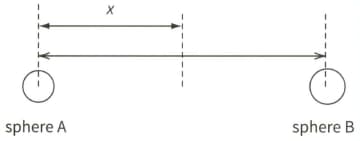
Sphere A carries a charge of $+2.0\times {10}^{-9}C$.

The graph shows how the electric field strength between the two spheres varies with distance $x$.

Determine the field strength 5.0cm from the centre of sphere A.

Two charged conducting spheres, each of radius $1.0 \mathrm{~cm}$, are placed with their centres $10 \mathrm{~cm}$ apart, as shown.

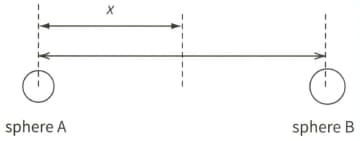
Sphere A carries a charge of $+2.0\times {10}^{-9}C$.

The graph shows how the electric field strength between the two spheres varies with distance $x$.

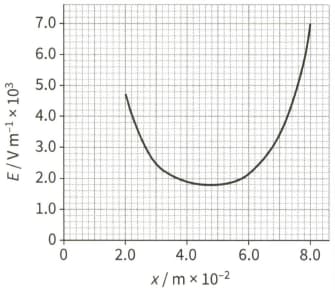
(ii) Use your result to ito calculate the charge on sphere B.

Two charged conducting spheres, each of radius $1.0 \mathrm{~cm}$, are placed with their centres $10 \mathrm{~cm}$ apart, as shown.

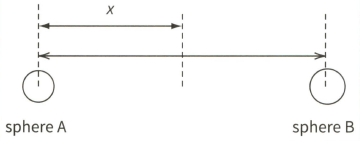
Sphere A carries a charge of $+2.0\times {10}^{-9}C$.

(c) (i) Sphere B is now removed. Calculate the potential at the surface of sphere A.

Two charged conducting spheres, each of radius $1.0 \mathrm{~cm}$, are placed with their centres $10 \mathrm{~cm}$ apart, as shown.

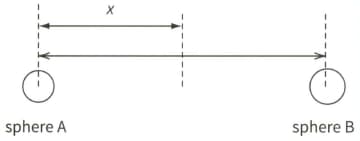
Sphere A carries a charge of $+2.0\times {10}^{-9}C$.

(c) (ii)Suggest and explain how the potential at the surface of sphere A would compare before and after sphere B was removed.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$. Calculate the potential difference that an $\alpha$-particle, initially at rest, would have to be accelerated through to gain this energy.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$. Calculate the speed of the a-particle at this kinetic energy.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$.

(b) This diagram shows the path of an $\alpha$-particle of this energy as it approaches a gold nucleus head-on.

(i) State the speed of the $\alpha$-particle at its point of closest approach to the gold nucleus.