The number of points of intersection of the diagonals of a regular hexagon is :

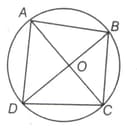
In the given figure $\mathrm{ABCD}$ is a cyclic quadrilateral, $\mathrm{DO}=8 \mathrm{cm}$ and $\mathrm{CO}=4 \mathrm{cm}$. $\mathrm{AC}$ is the angle bisector of $\angle \mathrm{BAD}$. The length of $\mathrm{AD}$ is equal to the length of $\mathrm{AB}. \mathrm{DB}$ intersects diagonal $\mathrm{AC}$ at $\mathrm{O}$, what is the length of the diagonal $\mathrm{AC} ?$

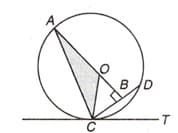
In the given diagram CT is tangent at C, making an angle of $\frac{\pi }{4}$ with CD. O is the centre of the circle. CD$=10$ cm. What is the perimeter of the shaded region ($\mathrm{\Delta }$ $\mathrm{AOC}$) approximately? 

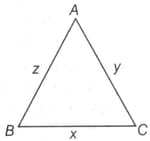
If ${\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2=\mathrm{xy}+\mathrm{yz}+\mathrm{zx},$ then the triangle is :

In the adjoining figure there are two congruent regular hexagons each with side $6 \mathrm{cm}.$ 

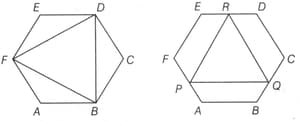
What is the ratio of area of $∆\mathrm{BDF}$ and $∆\mathrm{PQR},$ if $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ are the mid-points of side $\mathrm{AF}, \mathrm{BC}$ and $\mathrm{DE} ?$

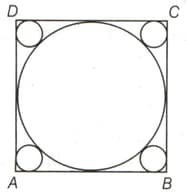
$\mathrm{ABCD}$ is a square, in which a circle is inscribed touching all the sides of a square. In the four corners of square $4$ smaller circles of equal radii are drawn, containing the maximum possible area. What is the ratio of the area of larger circle to that of sum of the areas of four smaller circles?

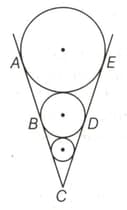
In the adjoining figure $\angle \mathrm{ACE}$ is a right angle. There are three circles which just touch each other where $\mathrm{AC}$ and $\mathrm{EC}$ are the tangents to all the three circles. What is the ratio of radii of the largest circle to that of the smallest circle?

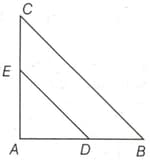
In a right angle triangle $\mathrm{ABC}, \angle \mathrm{A}$ is right angle, $\mathrm{DE}$ is parallel to the hypotenuse $\mathrm{BC}$ and the length of $\mathrm{DE}$ is $65\%$ the length of $\mathrm{BC},$ what is the area of $∆\mathrm{ADE},$ if the area of $∆\mathrm{ABC}$ is $68{ \mathrm{cm}}^2 ?$

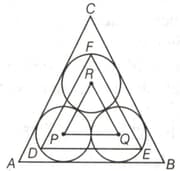
In the adjoining figure three congruent circles are touching each other. Triangle $\mathrm{ABC}$ circumscribes all the three circles. Triangle $\mathrm{PQR}$ is formed by joining the centres of the circle. There is a third triangle $\mathrm{DEF}.$. Points $\mathrm{A}, \mathrm{D}, \mathrm{P}$ and $\mathrm{B}, \mathrm{E}, \mathrm{Q}$ and $\mathrm{C}, \mathrm{F}, \mathrm{R}$ lie in the same straight lines respectively.

What is the ratio of perimeters of $∆\mathrm{ABC}:∆\mathrm{DEF}:∆\mathrm{PQR} ?$