The number of tangents that can be drawn to a circle from a point inside the circle is . (Write the answer in words)

Prove that the tangent and the radius through the point of contact of a circle are perpendicular to each other.

The radius of a circle with centre $O$ is $5 cm$. $P$ is a point at a distance $13 cm$ from $O$. $PQ$ and $PR$ are two tangents to this circle. Find the area of the quadrilateral $PQOR$.

From a point $P$ outside a circle, $PAB$ is a secant and $PT$ is a tangent to the circle, where $A, B$ and $T$ are points on the circle. If $PT=5 cm, PA=4 cm$ and $AB=x cm$, then $x$ is equal to :

In the figure, $O$ is the centre of the circle and $x^2+y^2=25$ is the equation of the circle. What is the radius of the circle?

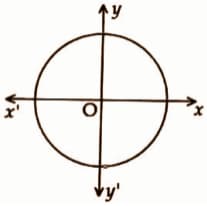
In the figure, $O$ is the centre of the circle and $x^2+y^2=25$ is the equation of the circle. Write the equation of the circle whose centre is at origin and the radius is $3$.

A line intersecting a circle in two points is called a secant.

The perpendicular drawn from the centre of a circle to a chord bisect the chord.

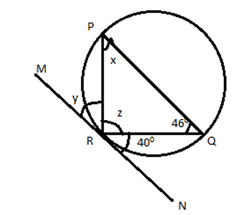
In the given figure, $\angle QRN=40°, \angle PQR=46°$ and $MN$ is a tangent at $R$. What is the value(in degrees) of $x, y$ and $z$ respectively?