EASY
Earn 100
The orthocenter is located inside the triangle in triangle. (Acute/Right)
100% studentsanswered this correctly
Important Questions on The Triangle and its Properties
EASY
MEDIUM
is an equilateral triangle of side , then length of one of its altitude is . The value of is _____.
MEDIUM
MEDIUM
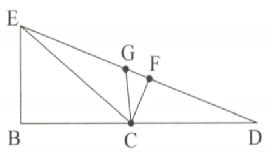
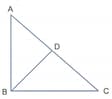
If is a right triangle, name the two altitudes of .
EASY
EASY
EASY
Write the definition of the altitude of a triangle.
EASY
MEDIUM
is ______
is _______
Is
EASY
MEDIUM
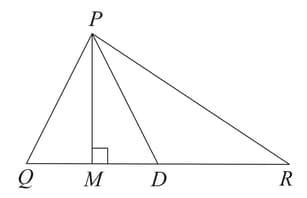
In , and are altitudes of the triangle.
HARD
EASY
EASY
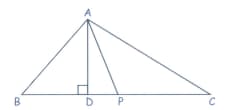
In the figure, identify the Altitude
EASY
Which of the following figures will have it's altitude outside the triangle?
MEDIUM
EASY
MEDIUM
HARD
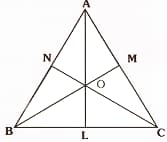
In the equilateral triangle , the three altitudes , , have been drawn that intersect at .
MEDIUM
Draw all three altitudes for the following triangles and explain how they are different: