EASY
Earn 100

The orthocentre of a right-angled triangle lies outside the triangle.

50% studentsanswered this correctly

Important Questions on Altitudes and Medians of a triangle

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
In ∆ABC, AB=AC and AL is perpendicular to BC at L. In ∆DEF, DE=DF and DM is perpendicular to EF at M. If (area of ∆ABC):(area of ∆DEF)=9.25, then DM+ALDM-AL is equal to:
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

The altitudes of a triangle intersect at _____.

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
In the given figure, lines l, m and n are called _______lines.
Question Image
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

Altitudes of a triangle meet at a point. The point is called _____.

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
Two or more lines that pass through the same point are called _____ lines.
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

Fill in the blanks.

Concurrent lines have a _____ point.

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
Three or more lines are ___, if they pass through a common point.
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
Three or more lines which pass through a single point are called _____ lines.
MEDIUM
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
In △ABC, D is the midpoint of BC.
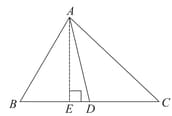
Question Image
AD is the _____.
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

Altitude of a triangle is the segment that is an _____ from a vertex on the opposite side.

MEDIUM
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively as shown in figure. The altitudes of the triangle are _____. (equal/unequal)
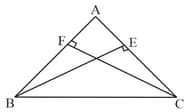
Question Image
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
The orthocenter is located on the vertex of the triangle in_____ triangle. (Acute/Right) 
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

 Two segments are concurrent only if they have_____common point. (One / Two / Infinite/ Zero)

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

A point where three or more lines meet is called:

 

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle

In the triangle ABC,

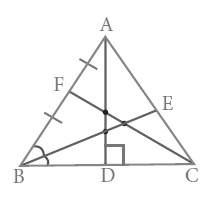
Question Image

The altitude is _____ .

EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
The orthocenter is located inside the triangle in _____ triangle. (Acute/Right) 
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
All diameters are concurrent at the _____ of the circle.
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
Two or more lines that pass through the same point are called _____ lines.
EASY
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
A perpendicular drawn from any vertex of a triangle to its opposite side is called a/an _____ (Base/Altitude/Hypotenuse)of the triangle.
MEDIUM
Mathematics>Geometry>Altitudes and Medians of a triangle>Altitude of a Triangle
In △ABC, D is the midpoint of BC.
Question Image
AE is the _____. (Median/ Altitude/ Perpendicular bisector/ Angle bisector)