The parametric equations of a curve are $x=t^2+6,y=t^4-t^3-5t$. The curve has a stationary point for a value of $t=1.394$.

Hence find the coordinates of the stationary point, giving each coordinate correct to $1$ significant figure.

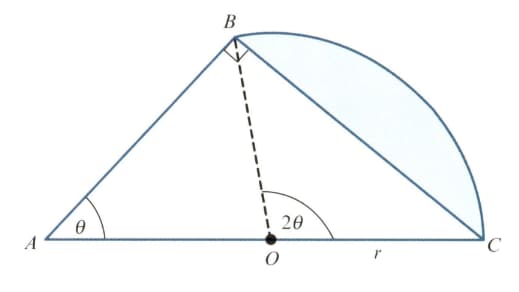
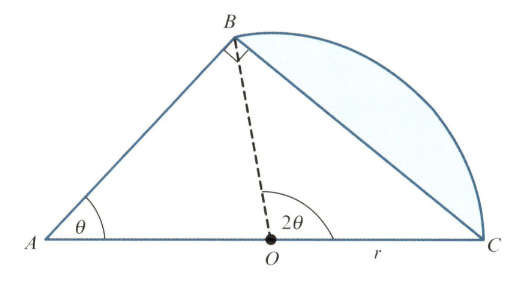
In the diagram, triangle $ABC$ is right-angled and angle $BAC$ is $\theta$ radians. The point $O$ is the mid point of $AC$ and $OC=r$. Angle $BOC$ is $2\theta$ radians and $BOC$ is a sector of the circle with centre $O .$ The area of triangle $ABC$ is $2$ times the area of the shaded segment.

Show that $\theta$ satisfies the equation $\sin 2\theta =\theta$.

In the diagram, triangle $ABC$ is right-angled and angle $BAC$ is $\theta$ radians. The point $O$ is the mid point of $AC$ and $OC=r$. Angle $BOC$ is $2\theta$ radians and $BOC$ is a sector of the circle with centre $O .$ The area of triangle $ABC$ is $2$ times the area of the shaded segment.

This equation has one root in the interval $0<\theta <\frac{\pi }{2}$. Use the iterative formula ${\theta }_{n+1}=\sin 2{\theta }_n$ to determine the root correct to $2$ decimal places. Give the result of each iteration to $4$ decimal places.

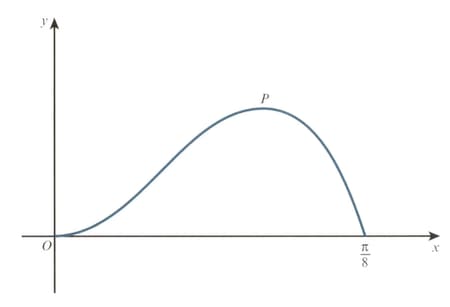
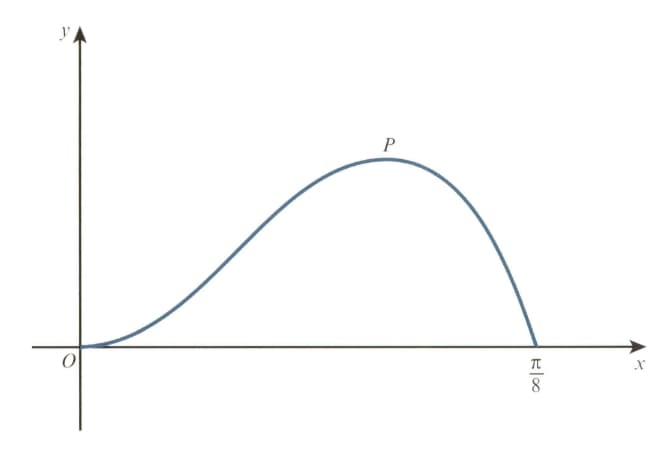
The diagram shows the curve $y=x^2\cos 4x$ for $0⩽x⩽\frac{\pi }{8}.$ The point $P$ is a maximum point.

Show that the $x$-coordinate of $P$ satisfies the equation $4x^2\tan 4x=2x$.

The diagram shows the curve $y=x^2\cos 4x$ for $0⩽x⩽\frac{\pi }{8}.$ The point $P$ is a maximum point.

Show also that the $x$ -coordinate of $P$ satisfies the equation $x=\frac{1}{4}{\tan }^{-1}\left(\frac{1}{2x}\right)$.

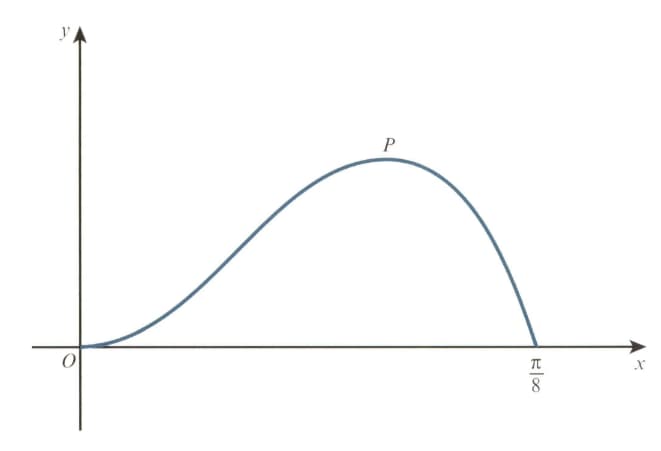
The diagram shows the curve $y=x^2\cos 4x$ for $0⩽x⩽\frac{\pi }{8}.$ The point $P$ is a maximum point.

Using an iterative formula based on the equation $x=\frac{1}{4}{\tan }^{-1}\left(\frac{1}{2x}\right)$ with initial value $x_1=0.3$. Find the $x$ -coordinate of $P$ correct to $2$ decimal places. Give the result of each iteration to $4$ decimal places.

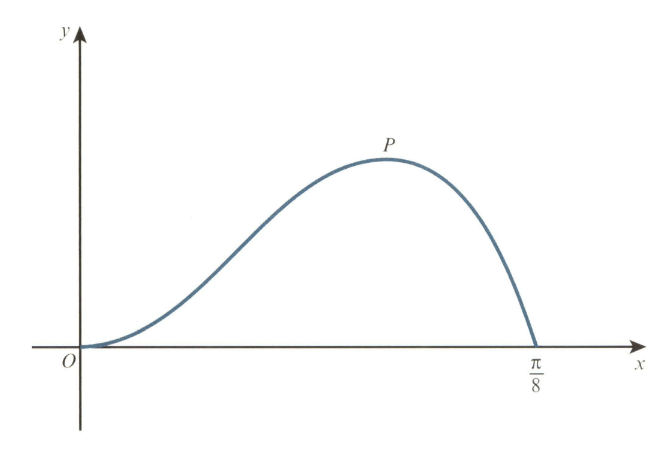
The diagram shows the curve $y=x^2\cos 4x$ for $0⩽x⩽\frac{\pi }{8}.$ The point $P$ is a maximum point.

Use integration by parts twice to find the exact area enclosed between the curve and the $x$ -axis from $0$ to $\frac{\pi }{8}$.

The terms of the sequence generated by the iterative formula $x_{n+1}=\frac{6}{7}\left(x_n+\frac{1}{{x_n}^3}\right)$ with initial value $x_1=1.5,$ converge to $\alpha .$

Use this formula to find $\alpha$ correct to $2$ decimal places. Give the result of each iteration to an appropriate number of decimal places.

The terms of the sequence generated by the iterative formula $x_{n+1}=\frac{6}{7}\left(x_n+\frac{1}{{x_n}^3}\right)$ with initial value $x_1=1.5,$ converge to $\alpha .$

State an equation satisfied by $\alpha ,$ and hence find the exact value of $\alpha .$