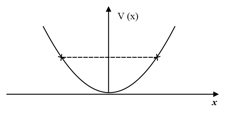
The potential energy function for a particle executing linear simple harmonic motion is given by $V\left(x\right)=\frac{k{x}^2}{2}$, where $k$ is the force constant of the oscillator. For $k=0.5 \mathrm{N} {\mathrm{m}}^{-1}$, the graph of $V\left(x\right)$ versus $x$ is shown in Fig. Show that a particle of total energy $1 \mathrm{J}$ moving under this potential must ‘turn back’ when it reaches $x=\pm 2 \mathrm{m}$.

(i) Dot product or scalar product of two vectors A and B is defined as $A.B= A\times B\times \cos \theta$, where θ is the angle between A and B

(ii) $A= A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$ and $B= B_x\hat{i}+B_y\hat{j}+B_z\hat{k}$ then, $A.B= A_x{B}_x+A_y{B}_y+A_z{B}_z$

(iii) Work done by a constant force, $W= \overrightarrow{F}.\overrightarrow{s}$

(iv) Work done by a variable force $dW= \overrightarrow{F}.d\overrightarrow{s}$

2. Relation between kinetic energy and momentum: 

Relation between momentum and kinetic energy, $KE= \frac{P^2}{2m}$ and $P= \sqrt{2m\times KE}$, where $P$ is linear momentum

3. Potential energy:

(i) Potential energy $\left(U\right)$ and force are related as, ${\int }_{U_1}^{U_2}dU= -{\int }_{r_1}^{r_2}\overrightarrow{F}.d\overrightarrow{r}$ i.e., $U_2-U_1= -{\int }_{r_1}^{r_2}\overrightarrow{F}.d\overrightarrow{r}=-W$ where $W$ is the work done by the conservative force.

(ii) Conservative force can be found from potential energy using the equation, $F\left(x\right)= -\frac{dU}{dx}$

4. Work energy theorem:

According to work-energy theorem, the net work done on a body is equal to the change in the kinetic energy, $W_{net}= \Delta KE$

5. Power:

(i) Power is the rate of work done, $P= \frac{dW}{dt}$

(ii) The average power delivered by an agent is given by $P_{av}= \frac{W}{t}$

(iii) Instantaneous power, $P= \frac{FdS}{dt}= F\frac{dS}{dt}= F.V$

6. Conservation of energy:

(i) According to conservation of mechanical energy, the total mechanical energy of an isolated system is conserved if the internal forces are conservative.

7. Collisions:

(i) The total momentum of a system remains constant during a collision.

(ii) Gravitational force and spring force are always non-impulsive during collision.

(iii) Total energy is conserved in an elastic collision.

(iv) The energy lost is maximum in a perfectly inelastic collision.

(v) The two equations which we can use in a collision are: $m_1{u}_1+m_2{u}_2= m_1{v}_1+m_2{v}_2$ and $e(u_1-u_2)= v_2-v_1$.

(vi) $e$ is the coefficient of restitution. It is $1$ for elastic collision, $0$ for perfectly inelastic collision and for inelastic collision it will be between $0$ and $1$.