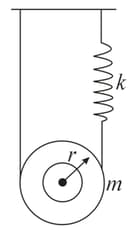
The pulley shown in figure has a radius $r,$ moment of inertia $I$ about its axis and mass $m.$ Find the time period of vertica oscillations of its center of mass. The spring constant of spring is $K$ and the spring does not slip over the pulley.

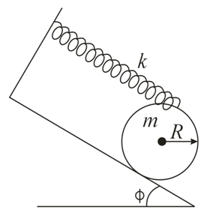
A uniform cylinder of mass $m$ and radius $R$ is in equilibrium on an inclined plane by the action of a light spring of stiffness $k,$ gravity and reaction force acting on it. If the angle of inclination of the plane is $\varphi ,$ find the angular frequency of small oscillation of the cylinder.

Assume that a tunnel is dug across the earth (radius $=R$ ) passing through its centre. Find the time a particle takes to cover the length of the tunnel if

(a) it is projected into the tunnel with a speed of $\sqrt{gR}$
(b) it is released from a height $R$ above the tunnel
(c) it is thrown vertically upward along the length of tunnel with a speed of $\sqrt{gR}$

a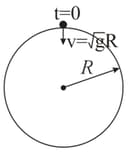 

b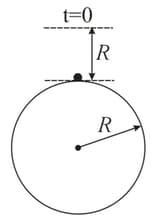 

c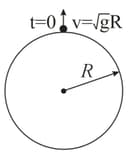 

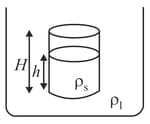
Consider a solid cylinder of density ${\rho }_s,$ cross-sectional area $A$ and height $h$ floating in a liquid of density ${\rho }_p,$ as shown in the given figure $\left({\rho }_l>{\rho }_s\right).$ It is depressed slightly and allowed to oscillate vertically. Find the frequency of small oscillations.

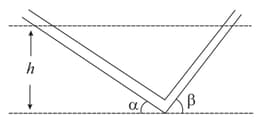
A $V$-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillations of liquid.

Two simple harmonic motions are represented by the following equations

$y_1=10\sin (\pi /4)(12t+1)$

$y_2=5(\sin 3\pi t+\sqrt{3}\cos 3\pi t)$

Here $t$ is in seconds.
Find out the ratio of their amplitudes. What are the time periods of the two motions?