For L. P. P, maximize z = 4 x 1 + 2 x 2 subject to 3 x 1 + 2 x 2 ≥ 9 , x 1 - x 2 ≤ 3 , x 1 ≥ 0 , x 2 ≥ 0 has ….

Infinite number of optimal solutions

The objective function Z = 4 x 1 + 5 x 2 , subject to 2 x 1 + x 2 ≥ 7 , 2 x 1 + 3 x 2 ≤ 15 , x 2 ≤ 3 & x 1 , x 2 ≥ 0 has minimum value at the point

On the line parallel to x − axis

EASY

Earn 100

The solution set of the inequation $3 x + 2 y > 3$ is

50% studentsanswered this correctly

Important Questions on Algebraic Inequalities

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

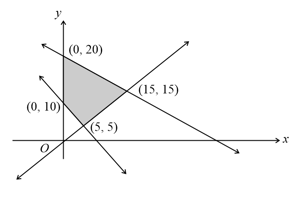
The feasible region of an LPP is shown in the figure. If

Z = 11 x + 7 y

, then the maximum value of

Z

occurs at

Question Image

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The maximum value of

Z = 4 x + 2 y

subject to constraints

2 x + 3 y \leq 18, x + y \geq 10

and

x, y \geq 0

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

Z = 7 x + y

subject to

5 x + y \geq 5, x + y \geq 3, x \geq 0, y \geq 0,

then the minimum value of

Z

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The minimum value of

z = 2 x_{1} + 3 x_{2}

z = 2 x_{1} + 3 x_{2}

subject to the constraints

2 x_{1} + 7 x_{2} \geq 22

x_{1} + x_{2} \geq 6, 5 x_{1} + x_{2} \geq 10

and

x_{1}, x_{2} \geq 0

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The maximum value of $z = 6 x + 8 y$ subject to $x - y \geq 0, x + 3 y \leq 12, x \geq 0, y \geq 0$ is

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The most correct statement is

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

Corner points of the feasible region determined by the system of linear constraints are

(0, 3), (1, 1)

and

(3, 0)

. Let

z = p x + q y

, where

p, q > 0

. Condition on

p

and

q

so that the minimum of

z

occurs at

(3, 0)

and

(1, 1)

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The minimum value of the function

Z = 2 x - y

, subjected to the constraints

x + y \leq 5, x + 2 y \geq 8, x \geq 0, y \geq 0

, is

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

For L. P. P, maximize

z = 4 x_{1} + 2 x_{2}

subject to

3 x_{1} + 2 x_{2} \geq 9, x_{1} - x_{2} \leq 3, x_{1} \geq 0, x_{2} \geq 0

has ….

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The coordinates of the point at which minimum value of

Z = 7 x - 8 y

subject to constraints

x + y - 20 \leq 0,

y \geq 5,

x \geq 0,

y \geq 0

is attained, is

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The feasible region of an $LPP$ is shown in the figure. If $z = 3 x + 9 y$ , then the minimum value of $z$ occurs at

Question Image

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

What is the area of the region enclosed by the inequalities

x \geq 0, y \geq 0, 4 x - y + 4 \leq 0

and

x - 3 y \geq 0 ?

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The corner points of the feasible region determined by the system of linear constraints are

(0, 10), (5, 5), (25, 20)

and

(0, 30) .

Let

Z = p x + q y,

where

p, q > 0 .

Condition on

p

and

q

so that the maximum of

Z

occurs at both the points

(25, 20)

and

(0, 30)

is _________.

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The L.P.P. to maximize

z = x + y,

subject to

x + y \leq 30, x \leq 15, y \leq 20, x + y \geq 15, x, y \geq 0

has

EASY

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The corner points of the feasible region determined by the system of linear constraints are

(0, 10), (5, 5), (15, 15), (0, 20) .

Let

Z = p x + q y

where

p, q > 0

. Condition on

p

and

q

so that the maximum of

z

occurs at both the points

(15, 15)

and

(0, 20)

, is

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

A furniture trader deals in only two items - chairs and tables. He has $50, 000$ rupees to invest and a space to store at most $35$ items. A chair costs him $1000$ rupees and a table costs him $2000$ rupees . The trader earns a profit of $150$ rupees and $250$ rupees on a chair and table, respectively. Formulate the above problem as an LPP to maximise the profit and solve it graphically.

MEDIUM

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

Consider a Linear Programming Problem:
Minimize

Z = 5 x + 3 y

Subject to :

3 x + y \geq 10, 2 x + 2 y \geq 14

and

x + 2 y \geq 9 .

Which one of the following points lies outside the feasible region?

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The maximum value of

z = 9 x + 13 y

subject to constraints

2 x + 3 y \leq 18, 2 x + y \leq 10, x \geq 0, y \geq 0

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

The objective function

Z = 4 x_{1} + 5 x_{2},

subject to

2 x_{1} + x_{2} \geq 7, 2 x_{1} + 3 x_{2} \leq 15, x_{2} \leq 3 & x_{1}, x_{2} \geq 0

has minimum value at the point

HARD

Mathematics>Algebra>Algebraic Inequalities>Graphical Solution of Linear Inequalities in Two Variable

A system of linear equations in two variables,

p

and

q,

is given as

(n + 1) p + (n + 2) q = 8,

p - (n + 1) q + (n + 2) = 0, p + q = 3 .

Which of the following would be one of the values of

n

for which the given system of linear equations is consistent?

The solution set of the inequation 3x+2y>3 is

Important Questions on Algebraic Inequalities

Learn and Prepare for any exam you want !

The solution set of the inequation $3 x + 2 y > 3$ is