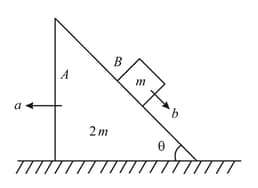
The system shown in figure is released from rest. Calculate the value of accelerations $a$ and $b$ (where $b$ is with respect to $A$)

 

What will be the value $M$ of the hanging block as shown in the figure which will prevent the smaller block from slipping over the triangular block. All the surface are frictionless and the string and the pulley are light.

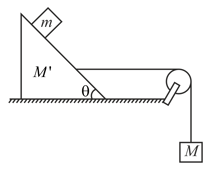
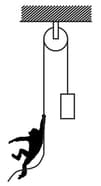
Figure shown a monkey is climbing on a rope that goes over a smooth light pulley and a block of equal mass hanging on the other end. Show that the monkey and the block move in the same direction with equal acceleration, whatever force the monkey exerts on the rope If initially both were at rest, their separation will not change as time passes.

In the arrangement shown in the figure, a wedge of mass $m^3=3.45 \mathrm{kg}$ is placed on a smooth horizontal surface. A small and light pulley is connected on its top edge as shown. A light flexible thread passes over the pulley. Two blocks having mass $m_1=1.3 \mathrm{kg}$ and $m_2=1.5 \mathrm{kg}$ are connected at the ends of the thread. $m_1$ is on smooth horizontal surface and $m_2$ rests on inclined surface of the wedge. Base length of the wedge is $2 m$ and inclination is $370. m_2$ is initially near the top edge of the wedge. If the whole system is released from rest. Calculate:

 (i) velocity of wedge when $m_2$ reaches its bottom
(ii) velocity of $m_2$ at that instant and tension in the thread during motion of $m_2$. All the surfaces are smooth $[ g=10 \mathrm{m} {\mathrm{s}}^{-2}]$

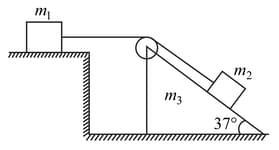
Neglecting friction every where, find the acceleration of $M$. Assume $m>m\text{'}$.

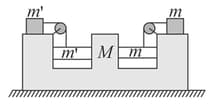
In the figure shown $P_1$ and $P_2$ are massless pulleys. $P_1$ is fixed and $P_2$ can move. Masses of $A, B$ and $C$ are $\frac{9m}{64} , 2m$ and $m$, respectively. All contacts are smooth and the string is massless. $\theta = {\tan }^{–1}\left(\frac{3}{4}\right)$. Find the acceleration of block $C$ in $\mathrm{m} {\mathrm{s}}^{-2}$.

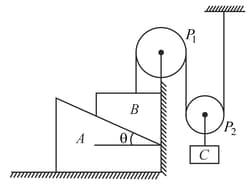
A system is shown in the figure. All contact surfaces are smooth and string is tight and inextensible. Wedge $A$ moves towards right with speed $10 \mathrm{m} {\mathrm{s}}^{-1}$ and velocity of $B$ relative to $A$ is in downward direction along the incline having magnitude $5 \mathrm{m} {\mathrm{s}}^{-1}$. Find the horizontal and vertical components of the velocity of block $C$.

An object of mass $2 \mathrm{kg}$ is placed at rest in a frame $\left(S_1\right)$ moving with velocity $10\hat{\mathrm{i}} + 5\hat{\mathrm{j}} {\mathrm{ms}}^{-1}$ and having acceleration $5\hat{\mathrm{i}} +10\hat{\mathrm{j}} {\mathrm{ms}}^{-2}$. This object is also seen by an observer standing in a frame $\left(S_2\right)$ moving with velocity $5\hat{\mathrm{i}}+10\hat{\mathrm{j}} {\mathrm{ms}}^{-1}$.

(i) Calculate ‘Pseudo force’ acting on object. Which frame is responsible for this force.

(ii) Calculate net force acting on object with respect to $S_2$ frame.

(iii) Calculate net force acting on object with respect to $S_1$ frame.