The terms of a sequence, defined by the iterative formula converge to the value The first term of the sequence is
The value is a root of an equation of the form Find this equation.

Important Questions on Numerical Solutions of Equations
The equation has a root, between and
Show that also satisfies the equation
The equation has a root, between and
Root also satisfies the equation .
Using an iterative formula based on the equation with a suitable starting value, find the value of correct to significant figures. Give the result of each iteration to significant figures.
The graphs of and intersect at the points and
Sketch these graphs on the same diagram.
The graphs of and intersect at the points and
Using logarithms, find a suitable iterative formula that can be used to find the coordinates of the point
The graphs of and intersect at the points and
Calculate the length of the line giving your answer correct to significant figures . Give the value of any iterations you calculate to a suitable number of significant figures.
The diagram shows a container in the shape of a cone with a cylinder on top.
The height of the cylinder is times its base radius,
The volume of the container must be The base of the cone has a radius of
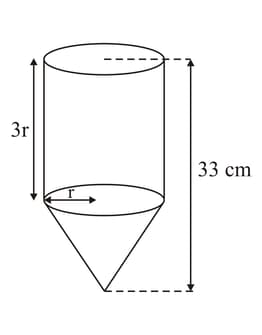
Write down an expression for the height of the cone in terms of
The diagram shows a container in the shape of a cone with a cylinder on top.
The height of the cylinder is times its base radius,
The volume of the container must be The base of the cone has a radius of
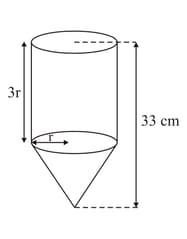
Show that .
The diagram shows a container in the shape of a cone with a cylinder on top.
The height of the cylinder is times its base radius,
The volume of the container must be The base of the cone has a radius of
.jpg)
Show that .
The equation has a root .
Show that is also a root of the equation
