MEDIUM

Earn 100

The total energy of a particle, executing simple harmonic motion is

50% studentsanswered this correctly

Important Questions on Oscillations

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

Total energy of a particle performing S.H.M. is NOT proportional to

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

The physical quantity conserved in simple harmonic motion is

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A body is executing S.H.M. Its potential energy is

E_{1}

and

E_{2}

at displacements

x

and

y

respectively. The potential energy at displacement

(x + y)

HARD

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

An object of mass

0.5 kg

is executing simple harmonic motion. It amplitude is

5 cm

and time period (T) is

0.2 s

. What will be the potential energy of the object at an instant

t = \frac{T}{4} s

starting from mean position. Assume that the initial phase of the oscillation is zero.

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A simple pendulum of length

L

has mass

M

and it oscillates freely with amplitude

A

. At the extreme position, its potential energy is (

g

= acceleration due to gravity)

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

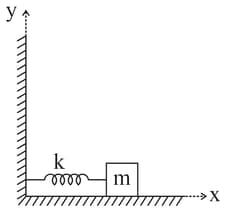
An object of mass $4 kg$ is attached to a spring which is fixed at one end on a rigid support and the mass-spring system is kept on a frictionless table. The object is allowed to execute simple harmonic motion along $X$ - direction. The force constant of the spring is $10 N m^{- 1}$ and the spring is stretched initially a distance of $5 cm$ , the total energy stored in the system is

Question Image

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

The total energy of a body executing simple harmonic motion is

E

. The kinetic energy when the displacement is

1 / 3

of the amplitude

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A body is executing simple harmonic motion with frequency

n

, the frequency of its potential energy is

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

The maximum value attained by the tension in the string of a swinging pendulum is four times the minimum value it attains. There is no slack in the string. The angular amplitude of the pendulum is

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A body of mass $1 kg$ is executing simple harmonic motion. Its displacement $y (cm)$ at $t$ seconds is given by $y = 6 \sin (100 t + \frac{π}{4})$ . Its maximum kinetic energy is

HARD

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

In a simple harmonic oscillation, what fraction of total mechanical energy is in the form of kinetic energy, when the particle is midway between mean and extreme position.

HARD

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

For a simple pendulum, a graph is plotted between its kinetic energy (K.E.) and potential energy (P.E.) against its displacement d. which one of the following represents these correctly? (graphs are schematic and not drawn to scale)

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A particle starts executing simple harmonic motion

(SHM)

of amplitude

a

and total energy

E .

At any instant, its kinetic energy is

\frac{3 E}{4}

, then its displacement

y

is given by:

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

For what value of displacement the kinetic energy and potential energy of a simple harmonic oscillation become equal?

EASY

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

Total energy of a particle of mass '

m

' executing SHM given by

y = A \sin ω t

for any displacement is:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A particle of mass

1 kg

is hanging from a spring of force constant

100 N m^{- 1} .

The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period

T .

The minimum time when the kinetic energy and potential energy of the system will become equal, is

\frac{T}{n} .

The value of

n

is ________.

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

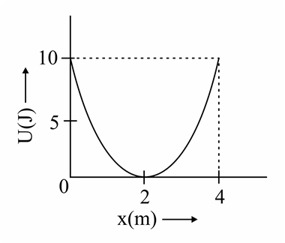
A mass of $5 kg$ is connected to a spring. The potential energy curve of the simple harmonic motion executed by the system is shown in the figure. A simple pendulum of length $4 m$ has the same period of oscillation as the spring system. What is the value of acceleration due to gravity on the planet where these experiments are performed ?

Question Image

HARD

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A potential is given by

V (x) = \frac{k (x + a)^{2}}{2}

for

x < 0

and

V (x) = \frac{k (x - a)^{2}}{2}

for

x > 0

. The schematic variation of oscillation period

T

for a particle performing periodic motion in this potential as a function of its energy

E

is:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A particle is executing simple harmonic motion with a time period

T

. At time

t = 0

, it is at its position of equilibrium. The kinetic energy - time graph of the particle will look like:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in Simple Harmonic Motion

A particle is executing simple harmonic motion

(S H M)

of amplitude

A,

along the

x

-axis, about

x = 0 .

When its potential Energy

(P E)

equals kinetic energy

(K E),

the position of the particle will be:

The total energy of a particle, executing simple harmonic motion is

Important Questions on Oscillations

Learn and Prepare for any exam you want !