The two parallel plates of a capacitor have equal and opposite charges $\mathrm{Q}$. The dielectric (which is filled between the capacitor plates) has a dielectric constant $\mathrm{K}$ and resistivity $\rho$.Show that the initially "leakage" current carried by the dielectric is given by the relationship $\mathrm{i}=\frac{\mathrm{Q}}{\mathrm{K}{\in }_0\mathrm{\rho }}$.

The parallel plates of a capacitor have an area $0.2 {\mathrm{m}}^2$ and are ${10}^{-2} \mathrm{m}$ apart. The original potential difference between them is $3000 \mathrm{V}$, and it decreases to $1000 \mathrm{V}$ when a sheet of dielectric is inserted between the plates filling the full space. Compute: (${\in }_0$ $= 9 \mathrm{x} {10}^{-12}$ S. I. units) 

$\left(\mathrm{i}\right)$ Original capacitance ${\mathrm{C}}_0$.

$\left(\mathrm{ii}\right)$ The charge $\mathrm{Q}$ on each plate.

$\left(\mathrm{iii}\right)$ Capacitance $\mathrm{C}$ after insertion of the dielectric.

$\left(\mathrm{iv}\right)$ Dielectric constant $\mathrm{K}.$

$\left(\mathrm{v}\right)$ Permittivity $\in$ of the dielectric.

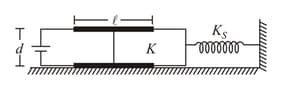
Consider the situation shown in figure. The width of each plate is $b$. The capacitor plates are rigidly clamped in the laboratory and connected to a battery of $\mathrm{emf}$ $V$. All surface are frictionless. Calculate the extension in the spring in equilibrium (spring is nonconducting).

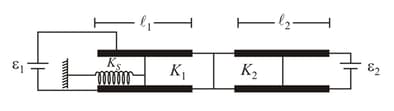
In figure shown, two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is same for the two capacitors. The plates are rectangular with width $b$ and lengths $l_1 \text{and} l_2$, the separation between plates is $d$. The left half of the dielectric slab has a dielectric constant $K_1$ and the right half ${\mathrm{K}}_2$ $(K_2>K_1)$. EMF of the right battery is greater than left battery. Neglecting any friction, find the extension in spring in equilibrium (spring is nonconducting) $({\mathrm{\epsilon }}_2>{\mathrm{\epsilon }}_1)$

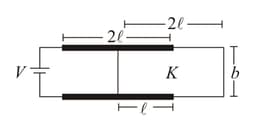
The plates of the parallel plate capacitor have plate area $A$ and are clamped in the laboratory as shown in figure. The dielectric slab of mass $m$, length $2l$ and width $2l$ is released from rest with length $l$ inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period. (plates of capacitor are square plates of side $2l$)

A parallel plate capacitor is filled with a dielectric up to one half of the distance between the plates. The manner in which the potential between the plates varies with distance is illustrated in the figure. Which half $(1\text{ or} 2)$ of the space between the plates is filled with the dielectric and what will be the distribution of the potential after the dielectric is taken out of the capacitor provided that

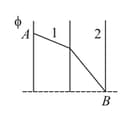
$\left(\mathrm{a}\right)$ The charges on the plates are conserved or

$\left(\mathrm{b}\right)$ The potential difference across the capacitor is constant.