The two plates of a parallel plate capacitor are $5 \mathrm{mm}$ apart. A slab of a dielectric, of thickness $4 \mathrm{mm}$ is introduced between the plates with its faces parallel to them. The distance between the plates is adjusted so that the capacitance of the capacitor becomes equal to its original value. If the new distance between the plates equal $8 \mathrm{mm}$, what is the dielectric constant of the dielectric used?

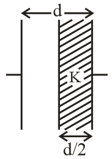
A parallel plate capacitor having cross-sectional area $A$ and separation $d$ has air in between the plates. Now an insulating slab of the same area but the thickness, $\frac{d}{2}$, is inserted between the plates as shown in figure having dielectric constant $K(=4).$ The ratio of new capacitance to its original capacitance will be,

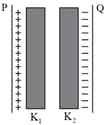
A parallel plate capacitor of two plates, each with area $90\pi {\mathrm{cm}}^2$, is separated by $5 \mathrm{mm}$ air-gap. The capacitor is initially connected to $100 \mathrm{V}$ source. When an unknown liquid is filled between the plates so as to fill the air-gap, an additional charge of $95 \mathrm{nC}$ is found to be flowing onto the capacitor from the $100 \mathrm{V}$ source. The dielectric constant of the liquid is
(Assume $\frac{1}{4\pi {ϵ}_0}=9\times {10}^9 \mathrm{N} {\mathrm{m}}^2 {\mathrm{C}}^{-2}$)

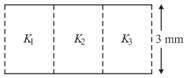
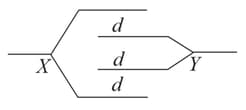
Four metallic plates each of area $A$ and separated from one another by a distance $d$ are arranged as shown in the figure. What is the capacitance between $X$ and $Y ?$

A parallel plate capacitor is made of two circular plates separated by a distance of 5 mm and with a dielectric of dielectric constant 2.2 between them. When the electric field in the dielectric is $3\times 10^4\text{ V/m}$, the charge density of the positive plate will be close to :

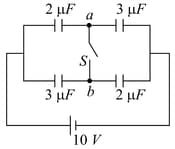
In the figure is shown a system of four capacitors connected across a $10 \mathrm{V}$ battery. The charge that will flow from switch S when it is closed is: