MEDIUM

Earn 100

The value of $b$ for which the area bounded by the parabolas $y = x - b x^{2}$ and $y = \frac{1}{b} x^{2}, b > 0$ is maximum, is equal to

50% studentsanswered this correctly

Important Questions on Area under Curves

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The parabola

y^{2} = 4 x + 1

divides the disc

x^{2} + y^{2} \leq 1

into regions with areas

A_{1}

and

A_{2} .

Then

|A_{1} - A_{2}|

equals

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in square units) bounded by the curves $y = \sqrt{x}, 2 y - x + 3 = 0$ , $X$ -axis and lying in the first quadrant is

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in sq. unit) of the region described by

A = \{(x, y) : x^{2} + y^{2} \leq 1 and y^{2} \leq 1 - x\}

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

If the area of the region bounded by the curves,

y = x^{2}, y = \frac{1}{x}

and the lines

y = 0

and

x = t (t > 1)

1 sq . unit

, then

t

is equal to

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

If the area enclosed between the curves

y = k x^{2}

and

x = k y^{2}, (k > 0),

1 s q . u n i t .

Then

k

EASY

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area of region bounded by the lines

y = m x, x = 1

and

x = 2

and the

x

-axis is

7.5

sq. units, then

m

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in square units) of the region bounded by the curves

y + 2 x^{2} = 0

and

y + 3 x^{2} = 1

, is equal to

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area of the region bounded by the lines

y = 2 x + 1, y = 3 x + 1

and

x = 4

EASY

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in sq. units) of the region bounded by the parabola,

y = x^{2} + 2

and the lines,

y = x + 1, x = 0

and

x = 3

, is

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area of the region

A = {(x, y) : 0 \leq y \leq x |x| + 1 and - 1 \leq x \leq 1}

in sq. units, is

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

On the real line

R

, we define two functions

f

and

g

as follows:

f (x) = m i n {x - [x], 1 - x + [x]}

g (x) = m a x \{x - [x], 1 - x + [x]\}

Where

[x]

denotes the largest integer not exceeding

x

. The positive integer

n

for which

\int_{0}^{n} (g (x) - f (x)) d x = 100

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

Area of the region

{(x, y) \in R^{2} : y \geq \sqrt{|x + 3|},

5 y \leq x + 9 \leq 15}

is equal to

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area of the region bounded by the curve

y = |x^{3} - 4 x^{2} + 3 x|

and the

x

-axis,

0 \leq x \leq 3,

EASY

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area enclosed between the parabolas

y^{2} = 16 x

and

x^{2} = 16 y

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in sq. units) of the region

\{(x, y) : x \geq 0, x + y \leq 3, x^{2} \leq 4 y a n d y \leq 1 + \sqrt{x}\}

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

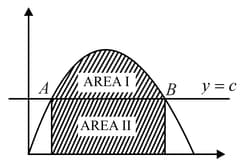
The figure shows a portion of the graph $y = 2 x - 4 x^{3} .$ The line $y = c$ is such that the areas of the regions marked $I$ and $II$ are equal. If $a, b$ are the $x$ -coordinates of $A, B$ respectively, then $a + b$ equals-

Question Image

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in sq. units) of the smaller portion enclosed between the curves,

x^{2} + y^{2} = 4

and

y^{2} = 3 x

, is:

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

A farmer

F_{1}

has a land in the shape of a triangle with vertices at

P (0, 0), Q (1, 1)

and

R (2, 0) .

From this land, a neighbouring farmer

F_{2}

takes away the region which lies between the side

P Q

and a curve of the form

y = x^{n}, n > 1

. If the area of the region taken away by the farmer

F_{2}

is exactly

30%

of the area of

∆ P Q R,

then the value of

n

MEDIUM

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

Let

I = \int_{a}^{b} (x^{4} - 2 x^{2}) d x .

I

is minimum then the ordered pair

(a, b)

HARD

Mathematics>Integral Calculus>Area under Curves>Area under the Curve

The area (in sq. units) of the region described by

[(x, y) : y^{2} \leq 2 x and y \geq 4 x - 1]

The value of b for which the area bounded by the parabolas y=x –bx2 and y=1bx2,b>0 is maximum, is equal to

Important Questions on Area under Curves

Learn and Prepare for any exam you want !

The value of $b$ for which the area bounded by the parabolas $y = x - b x^{2}$ and $y = \frac{1}{b} x^{2}, b > 0$ is maximum, is equal to