The value of $f\left(x\right)$ is given only at $x=0,\frac{1}{3},\frac{2}{3},1$. Which of the following can be used to evaluate${\int }_0^{1}f\left(x\right)dx$ approximately?

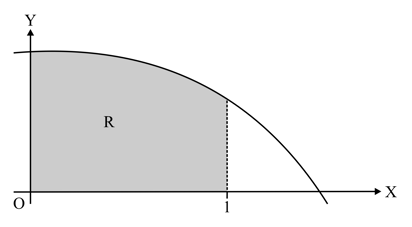
The diagram shows part of the curve $y=2-x^2\ln (x+1)$. The shaded region $R$ is bounded by the curve and by the lines $x=0,x=1\text{ and }y=0$. Use the trapezium rule with $4$ intervals to estimate the area of $R$ giving your answer correct to $2$ decimal places. State, with a reason, whether the trapezium rule gives an under-estimate or an over-estimate of the true value of the area of $R$. [Use, $\ln \left(1\right)=0,\ln \left(1.25\right)=0.223143551,\ln \left(1.5\right)=0.405465108,\ln \left(1.75\right)=0.559615788,\ln \left(2\right)=0.693147181$]

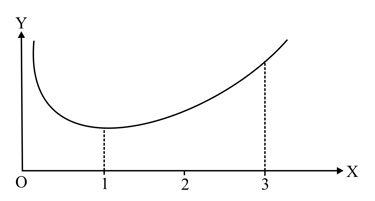
The diagram shows part of the curve $y=\frac{e^x}{2x}$. Use the trapezium rule with $4$ intervals to estimate the area of the shaded region, giving your answer correct to $2$ decimal places. State, with a reason, whether the trapezium rule gives an under-estimate or an over-estimate of the true value of the shaded area. [Use, $e=2.718$]