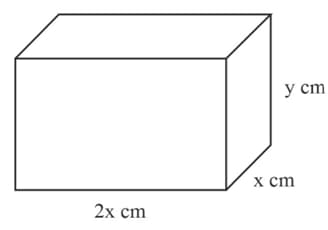
The volume of the solid cuboid shown in the diagram is and the surface area is . Find the minimum value of and state the dimensions of the cuboid for which this occurs.


Important Questions on Further Differentiation
A piece of wire, of lengthcm, is cut into two pieces.
one piece is bent to make a square of side cm and the other is bent to make a circle of radius cm
the total area enclosed by the two shapes is .
Express in terms of .
A piece of wire, of lengthcm, is cut into two pieces.
one piece is bent to make a square of side cm and the other is bent to make a circle of radius cm
the total area enclosed by the two shapes is .
Show that .
A piece of wire, of lengthcm, is cut into two pieces.
one piece is bent to make a square of side cm and the other is bent to make a circle of radius cm
the total area enclosed by the two shapes is .
Find the value of for which has a stationary value and determine the nature and magnitude of this stationary value.
A solid cylinder has radius cm and height cm.
The volume of this cylinder is and the surface area is .
Express in terms of .
A solid cylinder has radius and height .
The volume of the cylinder is and the surface area is .
Show that .
A solid cylinder has radius and height .
The volume of the cylinder is and the surface area is .
Find the value for for which there is a stationary value of .
A solid cylinder has radius and height .
The volume of the cylinder is and the surface area is .
Determine the magnitude and nature of this stationary value.
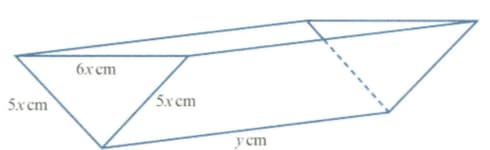
The diagram shows an open water container in the shape of a triangular prism of length .
The vertical cross-section is an isosceles triangle with sides . and .
The water container is made from of sheet metal and has a volume of .
Express in terms of .
