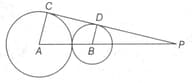
There are two tangents $\mathrm{AT}$ and $\mathrm{BT}$ on a circle of radius $30 \mathrm{cm}$. A line $\mathrm{OT}(=50 \mathrm{cm})$ connects the centre $\mathrm{O}$ with the external point $\mathrm{T}$. Another tangent $\mathrm{CD}$ touches the circle at $\mathrm{P}$ such that $\mathrm{C}$ and $\mathrm{D}$ lie on the line segments $\mathrm{AT}$ and $\mathrm{BT}$, respectively. Points $\mathrm{P}$ and $\mathrm{T}$ lie on the same side of the circle. Find the maximum possible area (in sq. $\mathrm{cm}$ ) of the circle inscribed in the triangle $\mathrm{CDT}$.

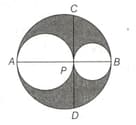
In the following figure there are two smaller circles inscribed in a larger circle touching each other. The centres of all the three circles fall on $\mathrm{AB}$, and $\mathrm{CD}$ is tangent to both the interior circles. If $\mathrm{CD}=16 \mathrm{cm}$, find the area of the shaded region.

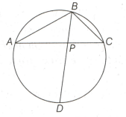
In the following figure $\mathrm{AB}=21 \mathrm{cm},\mathrm{BC}=15 \mathrm{cm},\mathrm{AC}=24 \mathrm{cm}.$ Point $\mathrm{P}$ is the mid-point of arc $\mathrm{AC}$, and the chord $\mathrm{BD}$ Bisects chord $\mathrm{AC}$ at $\mathrm{P}$. Find the ratio $\mathrm{BP} / \mathrm{PD}$.

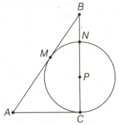
In the following figure one side of the $∆\mathrm{ABC}$ passes through the centre $\mathrm{P}$ of the circle and the other two sides of this triangle are tangents to this circle. If $\mathrm{BN}=2 \mathrm{cm}$ and $\mathrm{AC}=6 \mathrm{cm}$, find the radius of the circle.

In the following figure there are four chords $\mathrm{AB}, \mathrm{CD}, \mathrm{AC}, \mathrm{BD}$ in a circle. If $\mathrm{AB}=6, \mathrm{AP}=2, \mathrm{BP}=5$ $\mathrm{DP}=3$, find $\mathrm{CD}.$

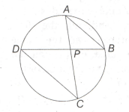
In a circle, its radius $\mathrm{OP}$ is intersected by a chord $\mathrm{AB}$ at $\mathrm{C}$, where $\mathrm{O}$ is the centre of the circle, such that $\mathrm{AC}=7, \mathrm{BC}=5$ and $\mathrm{PC}=1$, find the radius of the circle.

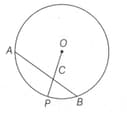
In a circle, its radius $\mathrm{OP}$ is extended to meet a point $\mathrm{A}$ outside the circle and a line segment $\mathrm{AB}$ is drawn from $\mathrm{A}$ to a point $\mathrm{B}$ on the circle. If $\mathrm{O}$ is the centre of the circle and $\mathrm{AP}=7, \mathrm{AB}=14$, find the circumference of the circle.

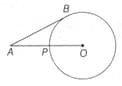
In the following diagram, there are two circles externally tangent to each other and there is a common tangent $\mathrm{CP}$ touch the circles at $\mathrm{C}$ and $\mathrm{D}·\mathrm{AC}$ and $\mathrm{BD}$ are the radii of the two circles. If $\mathrm{AC}=15$ and $\mathrm{BD}=6$, find the distance between $\mathrm{C}$ and $\mathrm{D}.$