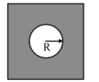
There is a uniform rectangular wire frame having a thin film of soap solution. A massless thin wire of radius $R$ and area of cross section $A$ is placed on the surface of film, and inside portion of the film is pricked. If surface tension of soap solution is $S$ and Young's modulus of wire is $Y$ then change in radius of the wire is:

A capillary, of the shape as shown, is dipped in a liquid. The contact angle between the liquid and the capillary is $0°$and the effect of liquid inside the meniscus is to be neglected. $T$is the surface tension of the liquid, $r$is the radius of the meniscus, $g$is the acceleration due to gravity and $\rho$is the density of the liquid. Then height $h$in equilibrium is

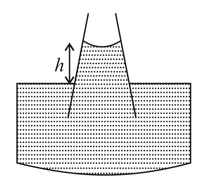
Two different vertical positions $\left(a\right)$ & $\left(b\right)$ of a capillary tube are shown in figure with the lower end inside water. For position $\left(a\right)$, contact angle is $\frac{\pi }{4}$ rad & water rises to height $h$ above the surface of water while for position $\left(b\right)$ height of the tube outside water is kept insufficient & equal to $\frac{h}{\sqrt{2}}$ ,then contact angle in radian becomes:

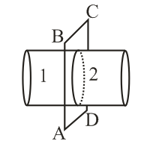
A water jet of radius $R$ is shown in the figure. The force between the part $1$ and part $2$ at the section $ABCD$ due to the surface tension is : (Assume that, $T$ is surface tension)

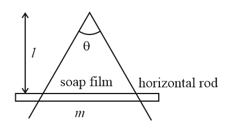
A wire is bend at an angle $\theta$. A rod of mass $m$ can slide along the bended wire without friction as shown in figure. If a soap film is maintained in the frame and frame is kept in a vertical position and rod is in equilibrium. If rod is displaced slightly in vertical direction. The time period of small oscillation is $a\pi \sqrt{\frac{bl}{g}}$ sec. where $a$ and $b$ are constant number then $a+b$ is

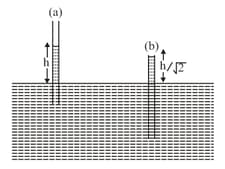
Consider a $\mathrm{U}$-shaped frame with a sliding wire of length $l$ and mass $m$ on its arm. It is dipped in a soap solution that taken out and placed in vertical position as shown in the figure. Choose a minimum value of $m$, so that the wire does not descend (surface tension of soap solution is $S$):

An oil drop falls through the air with a terminal velocity of $5 \times {10}^{–4} \mathrm{m} {\mathrm{s}}^{-1}$. The radius of the drop will be: $\eta =3.6\times {10}^{-5 }\mathrm{N} \mathrm{s} {\mathrm{m}}^{-2}, {\mathrm{\rho }}_{\mathrm{oil}}=900 \mathrm{kg} {\mathrm{m}}^{-3}$.,$g=10 \mathrm{m} {\mathrm{s}}^{-2}$

Neglect the density of air as compared to oil.