These are the speed-time graphs for two falling balls:

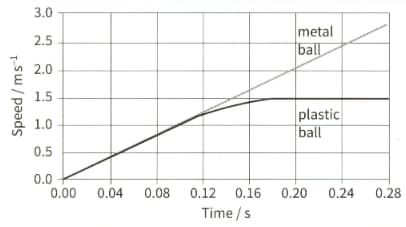
Explain why both balls have the same initial acceleration. 

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{m} \mathrm{s}}^{-1}$ in a time of $2.0 \mathrm{s}$. Calculate the forward driving force acting on the car while it is accelerating. Assume that, at low speeds, all frictional forces are negligible.

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{m} \mathrm{s}}^{-1}$ in a time of $2.0 \mathrm{s}$. At high speeds the resistive frictional force $\mathrm{F}$ produced by air on a body moving with velocity $\mathrm{v}$ is given by the equation $\mathrm{F}={\mathrm{bv}}^2$, where $\mathrm{b}$ is a constant. Derive the base units of force in the SI system.

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{ms}}^{-1}$ in a time of $2.0 \mathrm{s}$.

(b) At high speeds the resistive frictional force $\mathrm{F}$ produced by air on a body moving with velocity $\mathrm{v}$ is given by the equation $\mathrm{F}={\mathrm{bv}}^2$, where $\mathrm{b}$ is a constant.

(ii) Determine the base units of $\mathrm{b}$ in the SI system.

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{m} \mathrm{s}}^{-1}$ in a time of $2.0 \mathrm{s}$.  At high speeds the resistive frictional force $\mathrm{F}$ produced by air on a body moving with velocity $\mathrm{v}$ is given by the equation $\mathrm{F}={\mathrm{bv}}^2$, where $\mathrm{b}$ is a constant. The car continues with the same forward driving force and accelerates until it reaches a top speed of $50 \mathrm{m} {\mathrm{s}}^{-1}$. At this speed the resistive force is given by the equation $\mathrm{F}={\mathrm{bv}}^2$. Determine the value of $\mathrm{b}$ for the car.

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{m} \mathrm{s}}^{-1}$ in a time of $2.0 \mathrm{s}$. At high speeds the resistive frictional force $\mathrm{F}$ produced by air on a body moving with velocity $\mathrm{v}$ is given by the equation $\mathrm{F}={\mathrm{bv}}^2$, where $\mathrm{b}$ is a constant. Use your value of $\mathrm{b}$ and the driving force to calculate the acceleration of the car when the speed is $30{ \mathrm{m} \mathrm{s}}^{-1}$.

A car of mass $1200 \mathrm{kg}$ accelerates from rest to a speed of $8.0{ \mathrm{ms}}^{-1}$ in a time of $2.0 \mathrm{s}$. At high speeds the resistive frictional force $\mathrm{F}$ produced by air on a body moving with velocity $\mathrm{v}$ is given by the equation $\mathrm{F}={\mathrm{bv}}^2$, where $\mathrm{b}$ is a constant. Sketch a graph showing how the value of $\mathrm{F}$ varies with $\mathrm{v}$ over the range $0$ to $50 \mathrm{m}{\mathrm{s}}^{-1}$. Use your graph to describe what happens to the acceleration of the car during this time.

Explain what is meant by the mass of a body and the weight of a body.

 State and explain one situation in which the weight of a body changes while its mass remains constant.