These questions consist of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: In rotational plus translational motion of a rigid body different particles of the rigid body may have different velocities, but they will have same accelerations.
Reason: Translational motion of a particle is equivalent to the translational motion of a rigid body.

These questions consist of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: Two identical solid spheres are rotated from rest to the same angular velocity $\omega$ about two different axes as shown in the figure. More work will have to be done to rotate the sphere in case$-2.$

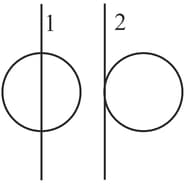
Reason: Moment of inertia in case$-2$ is more.

These questions consist of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: Angular momentum of sun and planet system about any point remains constant.

Reason: Two equal and opposite forces will act on them, the net torque of those two sets of forces about any point is zero.

These questions consists of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: Two identical spherical balls are released from two inclined planes. First is sufficiently rough and second is smooth. Both the balls will have same kinetic energy on reaching the bottom.

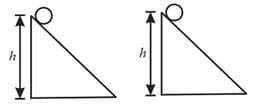
Reason: Linear velocity of second ball will be more.

A uniform circular disc of mass $50 \mathrm{kg}$ and radius $0.4 \mathrm{m}$ is rotating with an angular velocity of $10 \mathrm{rad} {\mathrm{s}}^{-1}$ about its own axis, which is vertical. Two uniform circular rings, each of mass $6.25 \mathrm{kg}$  and radius $0.2 \mathrm{m}\text{,}$ are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in $\mathrm{rad} {\mathrm{s}}^{-1}$) of the system is