This diagram shows the Earth's gravitational field.

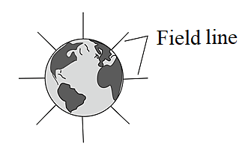
Copy the diagram and add arrows to show the direction of the field.  

This diagram shows the Earth's gravitational field.

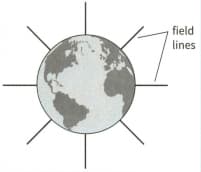
Explain why the formula for potential energy gained $\mathit{(}mg\mathit{∆}h\mathit{)}$ can be used to find the increase in potential energy when an aircraft climbs to a height of $10 000\mathrm{m}$, but cannot be used to calculate the increase in potential energy when a spacecraft travels from the Earth's surface to a height of $10 000 \mathrm{km}$.

Mercury, the smallest of the eight recognised planets, has a diameter of$4.88\times {10}^6\mathrm{m}$ $4.88\times {10}^6\mathrm{m}$and a mean density of $5.4\times {10}^3\mathrm{kg} {\mathrm{m}}^{-3}$. Calculate the gravitational field at its surface.

Mercury, the smallest of the eight recognised planets, has a diameter of$4.88\times {10}^6\mathrm{m}$ $4.88\times {10}^6\mathrm{m}$and a mean density of $5.4\times {10}^3\mathrm{kg} {\mathrm{m}}^{-3}$. A man has a weight of 900 N on the Earth's surface. What would his weight be on the surface of Mercury?

Ganymede is the largest of Jupiter's moons, with a mass of $1.48\times {10}^{23}\mathrm{kg}$. It orbits Jupiter with an orbital radius of $1.07\times {10}^6\mathrm{km}$ and it rotates on its own axis with a period of $7.15$ days. It has been suggested that to monitor an unmanned landing craft on the surface of Ganymede a geostationary satellite should be placed in orbit around Ganymede. Calculate the orbital radius of the proposed geostationary satellite.  

Ganymede is the largest of Jupiter's moons, with a mass of $1.48\times {10}^{23}\mathrm{kg}$. It orbits Jupiter with an orbital radius of $1.07\times {10}^6\mathrm{km}$ and it rotates on its own axis with a period of $7.15$ days. It has been suggested that to monitor an unmanned landing craft on the surface of Ganymede a geostationary satellite should be placed in orbit around Ganymede.

(b). Suggest a difficulty that might be encountered in achieving a geostationary orbit for this moon.

The Earth orbits the Sun with a period of $1$ year at an orbital radius of $1.50\times {10}^{11} \mathrm{m}.$ Calculate:

(a). The orbital speed of the Earth

The Earth orbits the Sun with a period of $1$ year at an orbital radius of $1.50\times {10}^{11} \mathrm{m}.$ Calculate the centripetal acceleration of the Earth.