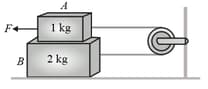
Three blocks are connected as shown in the figure. Calculate the minimum force required to move the body with constant velocity. The coefficient of friction at all surfaces is $0.25$.

  

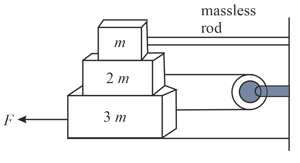
 [Assume that rod does not exert force in the vertical direction]

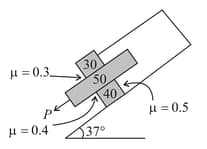
The three flat blocks in the figure, are positioned on the $37°$ incline and a force parallel to the inclined plane is applied to the middle block. The upper block is prevented from moving by a wire which attaches it to the fixed support. The masses of the three blocks in $\mathrm{kg}$ and coefficient of static friction for each of the three pairs of contact surfaces are shown in the figure. Determine the maximum value which force $P$ may have before the slipping take place anywhere.

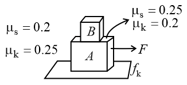
Block $B$ of mass $2 \mathrm{kg}$ rests on block $A$ of mass $10 \mathrm{kg}$. All surfaces are rough with the value of coefficient of friction, as shown in the figure. Find the minimum force $F$ that should be applied on block $A$ to cause relative motion between $A$ and $B$. $(g\mathrm{ }=10 \mathrm{m} {\mathrm{s}}^{-2})$

Two blocks $A$ and $B$ are as shown in the figure. The minimum horizontal force $F$ applied on the block $B$ for which slipping begins at $B$ and ground is:

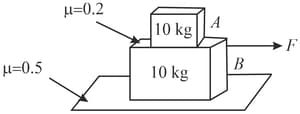
In the given diagram, what is the minimum value of a horizontal external force $F$ on the block $A$ so that block $B$ will slide on the ground?

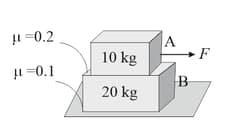
In the given diagram, what is the minimum value of a horizontal external force $F$ on the block $A$ so that block $B$ will slide on the ground?

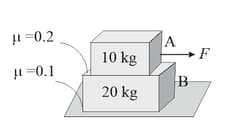
Two blocks $A\mathrm{ }\left(1\mathrm{ }\mathrm{kg}\right)$ and $B\mathrm{ }\left(2\mathrm{ }\mathrm{kg}\right)$ are connected by a string passing over a smooth pulley as shown in the figure. $B$ rests on a rough horizontal surface and $A$ rests on $B$. The coefficient of friction between $A$ and $B$ is the same as that between $B$ and the horizontal surface. The minimum horizontal force $F$ required to move $A$ to the left is $25\mathrm{ }\mathrm{N}.$ The coefficient of friction is

$(\mathrm{g}=10\mathrm{ }\mathrm{m} {{\mathrm{s}}^{-}}^2)\mathrm{ }$

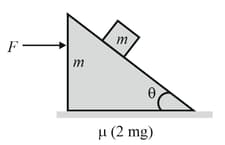
In the situation shown in the figure, a wedge of mass $m$ is placed on a rough surface, on which a block of equal mass is placed on the inclined plane of wedge. Friction coefficient between plane and the block and the ground and the wedge $\left(\mu \right)$. An external force $F$ is applied horizontally on the wedge. Given that $m$ does not slide on incline due to its weight. The value of $F$ at which wedge will start slipping is