In a ∆ A B C , if a 4 + b 4 + c 4 = 2 c 2 a 2 + b 2 , prove that C = 45 ° or 135 °

Given a 4 + b 4 + c 4 = 2 c 2 ( a 2 + b 2 ) c 4 + a 4 + b 4 − 2 a 2 c 2 − 2 b 2 c 2 = 0 Add and Subtract 2 a 2 b 2 c 4 + a 4 + b 4 − 2 a 2 c 2 − 2 b 2 c 2 + 2 a 2 b 2 − 2 a 2 b 2 = 0 ( c 2 − a 2 − b 2 ) 2 − ( 2 a b ) 2 = 0 We know this formula ( c 2 − a 2 − b 2 + 2 a b ) ( c 2 − a 2 − b 2 − 2 a b ) = 0 Used a 2 - b 2 Formula c 2 - a 2 - b 2 + 2 a b = 0 Or c 2 - a 2 - b 2 - 2 a b = 0 c 2 = a 2 + b 2 - 2 a b ⋯ 1 Or c 2 = a 2 + b 2 + 2 a b ⋯ 2 By cosine Rule c 2 = a 2 + b 2 - 2 a b cos C Compare the cosine formula equation 1 and equation 2 We get ⇒ cos C = ± 1 2 C = cos - 1 ± 1 2 ⇒ C = 45 o or 135 o Proved

In a ∆ A B C , if (i) sin A 2 sin B 2 sin C 2 > 0 (ii) sin A sin B sin C > 0 then

Both ( i ) and ( i i ) are true

Neither ( i ) nor ( i i ) is true.

If in a △ A B C , c 4 − 2 ( a 2 + b 2 ) c 2 + a 4 + a 2 b 2 + b 4 = 0 ,prove that C = 60 ° or 120 ° .

Given c 4 − 2 ( a 2 + b 2 ) c 2 + a 4 + a 2 b 2 + b 4 = 0 Add and subtract a 2 b 2 Rearrange the terms as c 4 + a 4 + b 4 − 2 a 2 c 2 − 2 b 2 c 2 + 2 a 2 b 2 − a 2 b 2 = 0 ( c 2 − a 2 − b 2 ) − a 2 b 2 = 0 we know the formula ⇒ ( c 2 − a 2 − b 2 + a b ) ( c 2 − a 2 − b 2 − a b ) = 0 used a 2 - b 2 formula c 2 − a 2 − b 2 + a b = 0 Or c 2 − a 2 − b 2 − a b = 0 then c 2 = a 2 + b 2 − a b c 2 = a 2 + b 2 + a b By cosine rule c 2 = a 2 + b 2 − 2 a b cos C cos C = ± 1 2 C = cos - 1 ± 1 2 C = 60 o and 120 o Proved

Find the value of a for the following figure [Use, cos 49 ° = 0 . 6560 . . . ]

Given that, we have, Using law of cosines, we have, a 2 = b 2 + c 2 - 2 b c cos A Therefore, a 2 = 5 2 + 7 2 - 2 × 5 × 7 × cos 49 ° ⇒ a 2 = 25 + 49 - 70 × cos 49 ° ⇒ a 2 = 74 - 70 × 0 . 6560 … ⇒ a 2 = 74 - 45 . 924 … ⇒ a 2 = 28 . 075 … ⇒ a = 28 . 075 … ⇒ a = 5 . 298 … ⇒ a = 5 . 30 [To two decimal places] Hence, the required value of a = 5 . 30 .

HARD

Earn 100

Through the mid - point of $M$ of the side $C D$ of a parallelogram $A B C D$ , the line $B M$ is drawn intersecting $A C$ in $L$ and $A D$ produced in $E$ . Then $E L =$

50% studentsanswered this correctly

Important Questions on Properties of Triangle

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

If two angles of

∆ A B C

are

\frac{π}{4}

and

\frac{π}{3}

, then the ratio of the smallest and the greatest side is

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In a triangle, if

r_{1} = 2 r_{2} = 3 r_{3}

, then

\frac{a}{b} + \frac{b}{c} + \frac{c}{a}

is equal to

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In a right triangle

A B C

, right angled at

A

, on the leg

A C

as diameter, a semicircle is described. The chord joining

A

with the point of intersection

D

of the hypotenuse and the semicircle, then the length

A C

equals to

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

D

is the midpoint of

B C

of a right-angled triangle

A B C, ∠ B A C = 90 °

such that triangle

A D C

is an equilateral

Δ

, then

a^{2} : b^{2} : c^{2}

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

The three sides of a triangle are given:

a = 8 cm, b = 6 cm, c = 7 cm

. Find the angle

A

. [Use

\cos^{- 1} (0.25) = 75.5224 \dots °

]

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In a

∆ A B C

, if

a^{4} + b^{4} + c^{4} = 2 c^{2} (a^{2} + b^{2})

, prove that

C = 45 °

135 °

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

Solve the triangle if $∠ B = 73 °, b = 51, a = 92$ . Round the angles and side lengths to the nearest $10^{th}$ . [Use $\sin 73 ° = 0.9563$ ]

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In the ambiguous case of the solution of triangle prove that the circumcircles of the two triangles are equal.

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In the given figure,

D E ∥ B C

and

A D : D B = 5 : 4

. Then

\frac{Ar (∆ D E F)}{Ar (∆ C B F)} = ?

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In a $∆ A B C,$ if

$(i) \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} > 0$

$(ii) \sin A \sin B \sin C > 0$ then

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

If in a triangle

A B C

, the altitude

A M

be the bisector of

∠ B A D

, where

D

is the mid-point of side

B C

, then prove that

(b^{2} - c^{2}) = \frac{a^{2}}{2}

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

A vertical lamp-post,

6 m

high, stands at a distance of

2 m

from a wall,

4 m

high. A

1.5 m

tall man starts to walk away from the wall on the other side of the wall, in line with the lamp-post. The maximum distance to which the man can walk remaining in the shadow is

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

If in a

△ A B C, c^{4} - 2 (a^{2} + b^{2}) c^{2} + a^{4} + a^{2} b^{2} + b^{4} = 0

,prove that

C = 60 °

120 °

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

Find the value of $a$ for the following figure

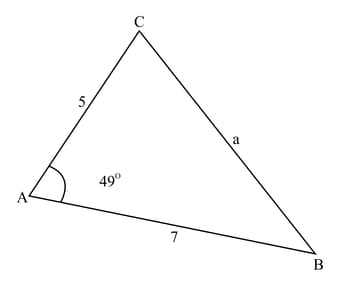
Question Image

[Use, $\cos 49 ° = 0.6560 . . .$ ]

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

In a

Δ ABC

, a, c and angle A are given and b₁, b₂ are two values of the third side b, such that b₂ = 2b₁, then sin A is

{a = B C, b = C A, c = A B}

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

ABC

is a right angled

Δ

in which

∠ B = 90 °

and

BC = a .

n

points

L_{1}, L_{2}, L_{3}, \dots, L_{n}

AB

are such that

AB

is divided into

(n + 1)

equal parts and

L_{1} M_{1}, L_{2} M_{2}, \dots L_{n} M_{n}

are line segments parallel to

BC

and points

M_{1}, M_{2}, \dots, M_{n}

are on

AC,

then the sum of the lengths of

L_{1} M_{1}, L_{2} M_{2}, \dots, L_{n} M_{n}

is:

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

Cotyledons are also called-

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

Represent the union of two sets by Venn diagram for each of the following.

$X = {x | x$ is a prime number between $80$ and $100}$

$Y = {y | y$ is an odd number between $90$ and $100}$

HARD

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

A square of side 'a' lies above the x -axis and has one vertex at the origin. The side passing through the origin makes an angle

α

(0 < α < π/4) with the positive direction of x -axis. The equation of its diagonal not passing through the origin is

EASY

Mathematics>Trigonometry>Properties of Triangle>Solution of Triangles

Δ A B C, B B_{1}

is the bisector of

∠ B .

Altitude drawn from

A

B B_{1}

meets side

B C

D_{1}

and

B B_{1}

D_{2}

. Value of

\frac{A D_{1}}{A D_{2}}

Through the mid - point of M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Then EL=

Important Questions on Properties of Triangle

Learn and Prepare for any exam you want !

Through the mid - point of $M$ of the side $C D$ of a parallelogram $A B C D$ , the line $B M$ is drawn intersecting $A C$ in $L$ and $A D$ produced in $E$ . Then $E L =$