Match the C p C v ratio for ideal gases with different type of molecules: Molecule Type C p / C v (A) Monoatomic (I) 7 / 5 (B) Diatomic rigid molecules (II) 9 / 7 (C) Diatomic non-rigid molecules (III) 4 / 3 (D) Triatomic rigid molecules (IV) 5 / 3

(A) – (IV), (B) – (I), (C) – (II), (D) – (III)

(A) – (IV), (B) – (II), (C) – (I), (D) – (III)

(A) – (III), (B) – (IV), (C) – (II), (D) – (I)

(A) – (II), (B) – (III), (C) – (I), (D) – (IV)

EASY

Earn 100

Total number of degrees of freedom of a rigid diatomic molecule is

50% studentsanswered this correctly

Important Questions on Kinetic Theory

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Given below are two statements:

Statement I: In a diatomic molecule, the rotational energy at a given temperature obeys Maxwell's distribution.

Statement II : In a diatomic molecule, the rotational energy at a given temperature equals the translational kinetic energy for each molecule.

In the light of the above statements, choose the correct answer from the options given below:

HARD

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Using equipartition of energy, the specific heat (in $J {kg}^{- 1} K^{- 1}$ ) of Aluminium at high temperature can be estimated to be (atomic weight of Aluminium $= 27$ )

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

The average energy of molecules in a sample of oxygen gas at

300 K

are

6.21 \times 10^{- 21}

J .

The corresponding values at

600 K

are

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

The ratio of the specific heats

\frac{C_{P}}{C_{v}} = γ

in terms of degrees of freedom

(n)

is given by:

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Molecules of an ideal gas are known to have three translational degrees of freedom. The gas is maintained at a temperature of

T

. The total internal energy,

U

of a mole of this gas, and the value of

γ = (\frac{C_{p}}{C_{v}})

are given, respectively, by

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

If one mole of the polyatomic gas is having two vibrational modes and

β

is the ratio of molar specific heats for polyatomic gas

(β = \frac{C_{P}}{C_{v}})

then the value of

β

is :

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

A man is climbing up a spiral staircase. His degrees of freedom are

HARD

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

The number of molecules in one litre of an ideal gas at

2

atmospheric pressure with mean kinetic energy

2 \times 10^{- 9} J

per molecule is:

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

The average thermal energy for a mono-atomic gas is : (

k_{B}

is Boltzmann constant and

T

, absolute temperature)

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

For a gas the value of

\frac{R}{C_{v}} = 0.4,

so the gas is
(R-Universal gas constant)

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

A polyatomic ideal gas has

24

vibrational modes. What is the value of

γ ?

MEDIUM

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

A gas mixture consists of

3

moles of oxygen and

5

moles of argon at temperature

T

. Assuming the gases to be ideal and the oxygen bond to be rigid, the total internal energy (in units of

R T

) of the mixutre is :

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Two ideal polyatomic gases at temperatures

T_{1}

and

T_{2}

are mixed so that there is no loss of energy. If

F_{1}

and

F_{2}, m_{1}

and

m_{2}, n_{1}

and

n_{2}

be the degrees of freedom, masses, number of molecules of the first and second gas respectively, the temperature of mixture of these two gases is:

MEDIUM

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Two moles of helium are mixed with n moles of hydrogen. If

\frac{C_{p}}{C_{v}} = \frac{3}{2}

for the mixture then the value of

n

is,

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

What will be the average value of energy along one degree of freedom for an ideal gas in thermal equilibrium at a temperature

T ?

(

k_{B}

is Boltzmann constant)

MEDIUM

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

What is the amount of heat needed to raise the temperature of the gas in a cylinder of fixed capacity (

44.8

litres) that contains helium gas at standard temperature and pressure, by

15.0 ° C

(R = 8.31 J {mol}^{- 1} K^{- 1})

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

What will be the average value of energy for a monoatomic gas in thermal equilibrium at temperature

T ?

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Pressure of an ideal gas is increased by keeping the temperature constant. The kinetic energy of molecules

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

Match the $\frac{C_{p}}{C_{v}}$ ratio for ideal gases with different type of molecules:

Molecule Type	$C_{p} / C_{v}$
(A) Monoatomic	(I) $7 / 5$
(B) Diatomic rigid molecules	(II) $9 / 7$
(C) Diatomic non-rigid molecules	(III) $4 / 3$
(D) Triatomic rigid molecules	(IV) $5 / 3$

EASY

Physics>Heat and Thermodynamics>Kinetic Theory>Law of Equipartition of Energy

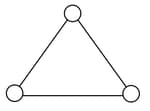
Question Image

Consider a gas of triatomic molecules. The molecules are assumed to be triangular and made of massless rigid rods whose vertices are occupied by atoms. The internal energy of a mole of the gas at temperature T is:

Total number of degrees of freedom of a rigid diatomic molecule is

Important Questions on Kinetic Theory

Learn and Prepare for any exam you want !