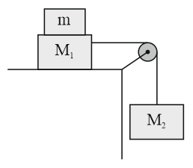
Two blocks of masses $M_1$ and $M_2$ are connected with a string passing over a pulley as shown in figure. The block $M_1$ lies on a horizontal surface. The coefficient of friction between the block $M_2$ and the horizontal surface is $\mu$. The system accelerates. What additional mass $m$ should be placed on the block $M_1$ so that the system does not accelerate?

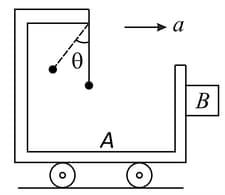
A trolley $A$ has a simple pendulum suspended from a frame fixed to its desk. A block $B$ is in contact on its vertical side. The trolley is on horizontal rails and accelerates towards the right$\left(a\right)$ such that the block is just prevented from falling. The value of coefficient of friction between $A$ and $B$ is  $0.5$. The inclination of the pendulum to the vertical is

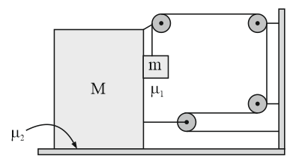
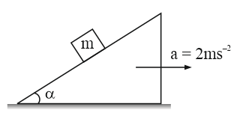
A block of mass $m$ is lying on a wedge having inclination angle $\alpha ={\tan }^{-1}\left(\frac{1}{5}\right)$. Wedge is moving with a constant acceleration $a=2 {\mathrm{ms}}^{-2}$. The minimum value of coefficient of friction $\mu$ so that $m$ remains stationary $\mathrm{w}.\mathrm{r}.\mathrm{t}.$wedge is

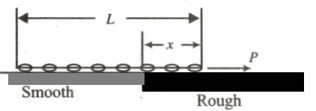
 A chain of length $L$ is placed on a horizontal surface as shown in figure. At any instant $x$ is the length of chain on rough surface and the remaining portion lies on smooth surface. Initially $x = 0$. A horizontal force $P$ is applied to the chain (as shown in figure). In the duration, $x$ changes from $x=0$ to $x=L$. For chain to move with constant speed,

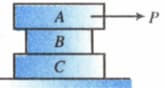
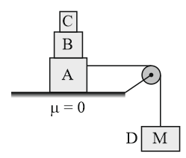
Find the least horizontal force $P$ to start motion of any part of the system of the three blocks resting upon one another as shown in figure. The weights of blocks are   $A=300 \mathrm{N}, B=100 \mathrm{N},$ and $C = 200 \mathrm{N}$. Between $A$ and $B$, the coefficient of friction is $0.3$, between $B$ and $C$ is  $0.2$, and between $C$ and the ground is  $0.1$.

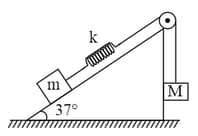
A block of mass $m$ is attached with a massless spring of force constant $k$. The block is placed over a rough inclined surface for which the coefficient of friction is $0.5. M$ is released from rest when the spring was unstretched. The minimum value of $M$, required to move the block $m$ up the plane is (neglect mass of string and pulley and friction in pulley)