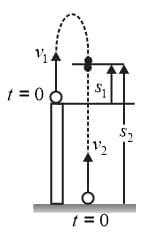
Two bodies $1$ and $2$ are projected simultaneously with velocities $v_1=2 \mathrm{m} {\mathrm{s}}^{-1}$ and $v_2=4 \mathrm{m} {\mathrm{s}}^{-1}$, respectively. The body $\mathrm{1 }$is projected vertically up from the top of a cliff of height $h=10 \mathrm{m}$ and the body $2$ is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in $\mathrm{s}$) of meeting of the bodies. 

  

A particle moves rectilinearly possessing a parabolic $s-t$ graph. Find the average velocity of the particle over a time interval from $t=\frac{1}{2} \mathrm{s}$ to $t=1.5 \mathrm{s}$.

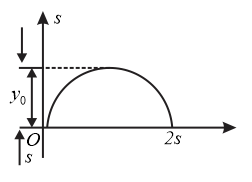
A particle moves in a straight line. Its position (in $\mathrm{m}$) as function of time is given by $x=\left(a{t}^2+b\right)$. What is the average velocity in time interval $t=3 \mathrm{s}$ to $t=5 \mathrm{s}$ in $\mathrm{m} {\mathrm{s}}^{-1}$? (Where $a$ and $b$ are constants and $a=1 \mathrm{m} {\mathrm{s}}^{-1}$, $b=1 \mathrm{m}$)

Find the sum of magnitudes of displacement in the pairs which give negative displacement in $\mathrm{m}$.

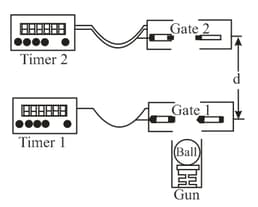
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upward by a gun. The ball passes electronic "gates" $1$ and $2$ as it rises and again as it falls. Each gate is connected to a separate timer. The first passage of the ball through each gate starts the corresponding timer, and the second passage through the same gate stops the timer. The time intervals $△t_1$ and $△t_2$ are thus measured. The vertical distance between the two gates is $d$. If $d=5 \mathrm{m}$, $△t_1=3 \mathrm{s}$, $△t_2=2 \mathrm{s}$, find the measured value of acceleration due to gravity . (in ${\mathrm{ms}}^{-2}$).