Two bodies of same mass tied with an inelastic string of length $l$ lie together. One of them is projected vertically upwards with velocity $\sqrt{6 gl}$. Find the maximum height up to which the centre of mass of system of the two masses rises.

A uniform thin rod of mass $M$ and length $L$ is standing vertically along $y-$axis on a smooth horizontal surface, with its lower end at the origin $(0,0)$. A slight disturbance at $t=0$ causes the lower end to slip on the smooth surface along the positive $X$-axis, and the rod starts falling.

(i) What is the path followed by the centre of mass of the rod during its fall?

A uniform thin rod of mass $M$ and length $L$ is standing vertically along $y$-axis on a smooth horizontal surface, with its lower end at the origin $(0,0)$. A slight disturbance at $t=0$ causes the lower end to slip on the smooth surface along the positive $X$-axis, and the rod starts falling.

(ii) Find the equation of the trajectory of a point on the rod located at a distance $r$ from the lower end. That is the shape of the path of this point?

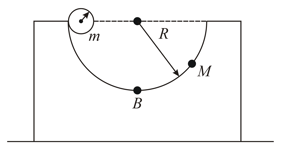
A block of mass $M$ with a semicircular track of radius $R$, rests on a horizontal frictionless surface. A uniform cylinder of radius $r$ and mass $m$ is released from rest at the top point $A$ (see Fig). The cylinder slips on the, semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point $B$) of the track? How fast is the block moving when the cylinder reaches the bottom of the track?

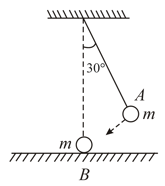
The bob $A$ of a pendulum released from $30°$ to the vertical hits another bob $B$ of the same mass at rest on a. table as shown in figure. How high does the bob A rise after the collision? Neglect the size of the bob and assume the collision to be elastic.

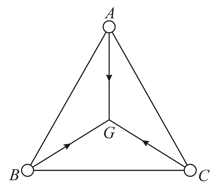
Three particles $A,B$ and $C$ of equal mass move with equal speed $v$ along the medians of an equilateral triangle as shown in figure. They collide at the centroid $G$ of the triangle. After the collision, $A$ comes to rest, $B$ retraces its path with the speed $v$. What is the velocity of $C$ ?

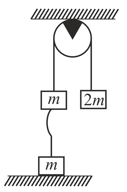
The Atwood machine in figure has a third mass attached to it by a limp string. After being released, the $2\mathrm{m}$ mass falls a distance $x$ before the limp string becomes taut. Thereafter both the mass on the left rise at the same, speed. What is the final speed? Assume that pulley is ideal.

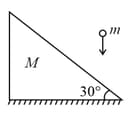
A ball of mass $m=1 \mathrm{kg}$ falling vertically with a velocity $v_0=2 \mathrm{m} {\mathrm{s}}^{-1}$ strikes a wedge of mass $M=2 \mathrm{kg}$ kept on a smooth, horizontal surface as shown in figure. The coefficient of restitution between the ball and the wedge is $e=\frac{1}{2}$. Find the velocity of the wedge and the ball immediately after collision.