EASY
Earn 100
Two congruent circles of centres and intersects each other at point and , then prove that .
(a)True
(b)False
77.78% studentsanswered this correctly
Important Questions on Circles
MEDIUM
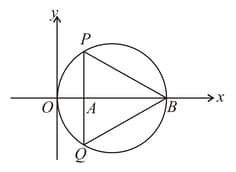
MEDIUM
HARD
MEDIUM
MEDIUM
The length of two chords and of a circle of centre are equal and then, is
HARD
HARD
Suppose are two unequal circles; and are the direct common tangents to these circles. A transverse common tangent cuts in and in . If units, then is -
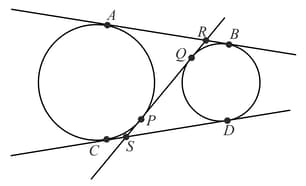
MEDIUM
EASY
EASY
MEDIUM
HARD
On the circle with center , points are such that . A point is located on the tangent at to the circle such that and are on the opposite sides of the line and . The line segment intersects the circle again at . Then the ratio is equal to -
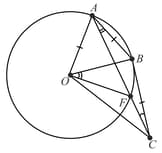
HARD
The two chords and of a circle are at equal distance from the centre . If and , then calculate the length of the radius of the circle.
HARD
MEDIUM
MEDIUM
In the given circle, with centre , are the mid-points of equal chords respectively. , then the value of is equal to
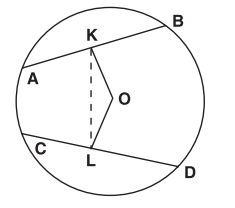
HARD
MEDIUM
MEDIUM
HARD

