Ten positively charged particles are kept fixed on the x-axis at points x = 10 cm , 20 cm , 30 cm . . . . . 100 cm . The first particle has a charge 1 .0 × 10 − 8 C , the second 8 × 10 − 8 C , third 27 × 10 − 8 C , and so on. The tenth particle has a charge 1000 × 10 − 8 C . Find the magnitude of the electric force acting on a 1 C charge placed at the origin.

Given that the charges are increased as, 1 3 × 10 - 8 C , 2 3 × 10 - 8 C , 3 3 × 10 - 8 C . . . . . . . . . . . . . . . . . . . . . 10 3 × 10 - 8 C Now, the net force on 1 C by all the charges on order is in the same direction. Hence, all forces on the given charges will be added to give the net amount of force on the charge. And the net force due to all the charges can be given by the vector sum of all the individual forces by the superposition principle. Using Coulomb's law for finding the interactive force between two charges let, q 1 , q 2 separated by a distance of r is given by, F = K q 1 q 2 r 2 Where, K = 9 × 10 9 N m 2 C - 2 is electrostatic constant Using the above expression for calculation of force between 1 C and 1 × 10 - 8 C Force, F 2 = K × 1 × 1 × 10 - 8 0 . 1 2 Similarly, the interactive force between 1 C and 8 × 10 - 8 C is, F 2 = K × 1 × 2 × 10 - 8 0 . 2 2 Similarly, F 3 = K × 1 × 27 × 10 - 8 0 . 3 2 To calculate the net force on the charge, F = F 1 + F 2 + F 3 + . . . . . . . . . . . + F 10 = K 1 × 10 - 8 0 . 1 2 + 8 × 10 - 8 0 . 2 2 + 27 × 10 - 8 0 . 3 2 + . . . . . . . . . . . . . . . . . . . + 1000 × 10 - 8 1 2 = K × 10 - 8 1 3 0 . 1 2 + 2 3 0 . 2 2 + 3 3 0 . 3 2 + . . . . . . . . . . . . . . . . . . . . . + 10 3 1 2 = K × 10 - 6 1 + 2 + 3 + . . . . . . . . . . . . . . . . . + 10 = K × 10 - 6 × 10 × 11 2 = 55 K × 10 - 6 = 55 × 9 × 10 9 × 10 - 6 = 4 . 95 × 10 5 N

EASY

12th CBSE

IMPORTANT

Earn 100

Two identical metallic spheres $A$ and $B$ , each carrying a charge $q$ , repel each other with a force $F$ . A third metallic sphere C of the same size, but uncharged, is successively made to touch the spheres $A$ and $B$ , and then removed away. What is the force of repulsion between $A$ and $B$ ?

Important Questions on Electric Charges and Field

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 14

Two point charges

+ 9 e

and

+ e

are kept at a distance

a

from each-other. Where should we place a third charge

q

on the line joining the two charges so that it may be in equilibrium?

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 15

Two point electric charges of values

q

and

2 q

are kept at a distance

d

apart from each other in air. A third charge

Q

is to be kept along the same line in such a way that the net force acting on

q

and

2 q

is zero. Calculate the position of charge

Q

in terms of

q

and

d

MEDIUM

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 16

A charge

q

is placed at the centre of the line joining two equal charges

Q

. Show that the system of three charges will be in equilibrium if

q = - \frac{Q}{4}

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 17

Two pith-balls each weighing

10^{- 3} kg

are suspended from the same point by means of silk threads

0.5 m

long. On charging the balls equally, they are found to repel each other to a distance of

0.2 m

. Calculate the charge on each ball.

MEDIUM

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 1

Ten positively charged particles are kept fixed on the x-axis at points

x = 10 cm, 20 cm, 30 cm . . . . . 100 cm

. The first particle has a charge

1 .0 \times 10^{- 8} C

, the second

8 \times 10^{- 8} C

, third

27 \times 10^{- 8} C

, and so on. The tenth particle has a charge

1000 \times 10^{- 8} C

. Find the magnitude of the electric force acting on a

1 C

charge placed at the origin.

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 2

Charges $q_{1} = 1.5 mC, q_{2} = 0.2 mC$ and $q_{3} = - 0 .5 mC$ are placed at the points $A$ , $B$ and $C$ respectively, as shown in Figure. If $r_{1} = 1 .2 m$ and $r_{2} = 0 .6 m$ calculate the magnitude of resultant force on $q_{2}$ .

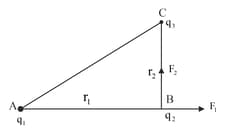
Question Image

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 3

Two equal positive charges, each of $2 μ C$ interact with a third positive charge of $3 μ C$ situated as shown in Fig. 1.32. Find the magnitude and direction of the force experienced by the charge of $3 μ C$ .

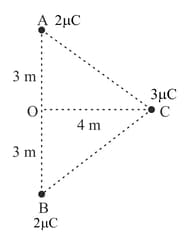
Question Image

EASY

12th CBSE

IMPORTANT

New Simplified Physics (Vol 1) For Class 12>Chapter 1 - Electric Charges and Field>Problems For Practice>Q 4

Four charges

+ q, + q, - q

and

- q

are placed respectively at the four corners

A, B, C

and

D

of a square of side

a

. Calculate the force on a charge

Q

placed at the centre of the square.

Two identical metallic spheres A and B, each carrying a charge q, repel each other with a force F. A third metallic sphere C of the same size, but uncharged, is successively made to touch the spheres A and B, and then removed away. What is the force of repulsion between A and B?

Important Questions on Electric Charges and Field

Learn and Prepare for any exam you want !