Two identical parallel plate capacitors are connected in parallel combination. Total charge on capacitors is $Q_{0}$. If one of the capacitors is kept in a dielectric medium of constant $k,$ then the total charge on both the capacitors will change to (P.D. across them is kept constant.)

The distance between the circular plates of a parallel plate condenser $40 \mathrm{mm}$ in diameter, in order to have same capacity as a sphere of radius $1 \mathrm{m}$ is

A parallel plate capacitor with air between the plates has a capacitance of $8 \mathrm{pF}$. The separation between the plates is now reduced by half and the space between them is filled with medium of dielectric constant $5$. The value of capacitance of a capacitor in the second case is

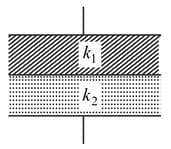
A parallel plate capacitor is filled with dielectric as shown in the figure. Its capacitance has a ratio with that without dielectric as

A parallel plate capacitor is charged to a certain potential difference. A slab of thickness $3 \mathrm{mm}$ is inserted between the plates and it becomes necessary to increase the distance between the plates by $2.4 \mathrm{mm}$ to maintain the same potential difference. The dielectric constant of the slab is

The capacity of a parallel plate condenser filled with material of dielectric constant $8$ is $16 \mathrm{\mu F}$. Its capacity, if the dielectric is removed, will be

Between the plates of a parallel plate condenser, a plate of thickness $t_{1}$ and dielectric constant $k_{1}$ is placed. In the rest of the space, there is another plate of thickness $t_{2}$ and dielectric constant $k_{2}$. The potential difference across the condenser will be

Capacitance of a capacitor made by a thin metal foil is $2 \mathrm{\mu F}$. If the foil is folded with paper of thickness $0.15 \mathrm{mm}$, dielectric constant of paper is $2.5$ and width of paper is $400 \mathrm{mm}$, then length of foil will be

A dielectric plate is introduced between the plates of a parallel plate capacitor to fill the space between the plates. The capacitor is charged and later disconnected from the battery. The dielectric plate is slowly drawn out of the capacitor parallel to the plates. The plot of the potential difference across the plates and the length of the dielectric plate drawn out is