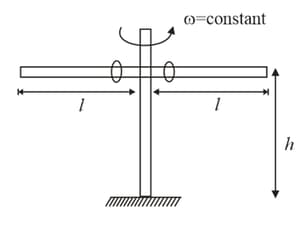
Two identical rings which can slide along the rod are kept near the midpoint of a smooth rod of length $2l(l=1 \mathrm{m})$ The rod is rotated with constant angular velocity $\omega =3 \mathrm{rad} {\mathrm{s}}^{-1}$ about the vertical axis passing through its center. The rod is at height $h=5 \mathrm{m}$ from the ground. Find the distance (in meter) between the points on the ground where the rings will fall after leaving the rods.

 

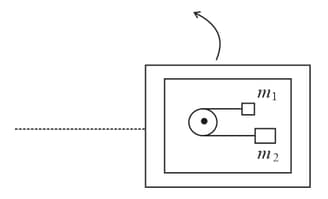
A table with the smooth horizontal surface is placed in a cabin which moves in a circle of a large radius $R$ (figure). A smooth pulley of a small radius is fastened to the table. Two masses $m$ and $2m$ placed on the table are connected through a string over the pulley. Initially, the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the value of $\frac{T}{ma}$, where $a$ is the magnitude of the initial acceleration of the masses as seen from the cabin and $T$ is the tension in the string.

A uniform square plate of mass m is supported as shown. If the cable suddenly breaks, determine just after that moment 

(a) The angular acceleration of the plate. 

(b) The acceleration of corner $C$.   

(c) The reaction at $A$.

Disk $A$ has a mass of $4 \mathrm{kg}$ and a radius $r=75 \mathrm{mm}$, it is at rest when it is placed in contact with the belt which moves at a constant speed $\nu =18 \mathrm{m} {\mathrm{s}}^{-1}.$ Knowing that ${\mu }_{\mathrm{k}}=0.25$ between the disk and the belt, determine the number of revolutions executed by the disk before it reaches a constant angular velocity. (Assume that the normal reaction by the belt on the disc is equal to weight of the disc). Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$

Three particles $A, B$ and $C$ each of mass $m$are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side $l$. This body is placed on a horizontal frictionless table ($x-y$ plane) and is hinged to it at the point $A$, so that it can move without friction about the vertical axis through $A$ as shown in the figure. The body is set into rotational motion on the table about $A$ with a constant angular velocity $\omega$.

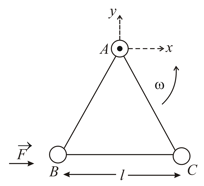
(a) Find the magnitude of the horizontal force exerted by the hinge on the body.

(b) At time $T,$ when the side $BC$ is parallel to the $x$-axis, a force $F$ is applied on $B$ along $BC$ as shown. Obtain the $x$-component and the $y$-component of the force exerted by the hinge on the body, immediately after time $T$.

A small spherical ball of mass $m$ is rolling without slipping down the loop track as shown in the figure. The ball is released from rest on the linear portion at a vertical height $h$ from the lowest point. The circular part as shown in figure has a radius $r. [g=10 \mathrm{m} {\mathrm{s}}^2 ]$

(a) Find the kinetic energy of the ball when it is at a point $A$, where the radius make an angle $\mathrm{\theta }$ with the horizontal.

(b) Find the radial and the tangential accelerations of the centre when the ball is at $A$.

(c) Find the normal force and the frictional force acting on the ball if $h=50 \mathrm{cm}, r=10 \mathrm{cm}, \mathrm{\theta }=0 \mathrm{and} m=70 \mathrm{g}.$

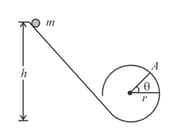
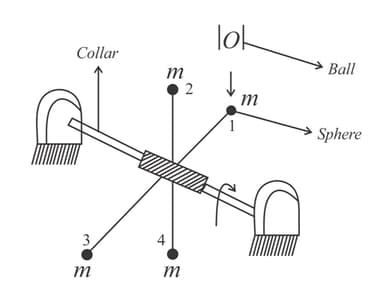
Figure $\left(1\right)$ shows a mechanical system free of any dissipation. The two spheres $(\mathrm{A} \mathrm{and} \mathrm{B})$ are each of equal mass $\mathrm{m}$, and a uniform connecting rod $\mathrm{AB}$ of length $2\mathrm{r}$ has mass $4\mathrm{m}$. The collar is massless. Right above the position of sphere $\mathrm{A}$ in Fig. $\left(1\right)$is a tunnel

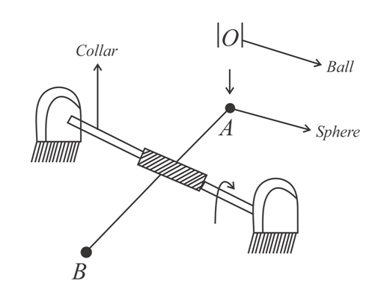
from which balls each of mass $\mathrm{m}$ fall vertically at suitable intervals. The falling balls cause the rods and attached spheres to rotate. Sphere $\mathrm{B}$ when reaches the position now occupied by sphere $\mathrm{A}$, suffers a collision from another falling ball and so on. Just before striking, the falling ball has velocity $\mathrm{\upsilon }$. All collision are elastic and the spheres as well as the falling balls can be considered to be point masses.

(a) Find the angular velocity ${\mathrm{\omega }}_{\mathrm{i} + 1 }$of the assembly in terms of$\left\{{\mathrm{\omega }}_{\mathrm{i}},\mathrm{\upsilon },\mathrm{and} \mathrm{r}\right\}$after the ${\mathrm{i}}^{\mathrm{th}}$ ball has struck it. ${\mathrm{\omega }}_{\mathrm{i}+1}$

(b) The rotating assembly eventually assumes constant angular speed ${\mathrm{\omega }}^{*}$. Obtain ${\mathrm{\omega }}^{*}$ in terms of $\mathrm{\upsilon }$ and $\mathrm{r}$ by solving the equation obtained in part (a). Argue how a constant ${\mathrm{\omega }}^{*}$ does not violate energy conservation. ${\mathrm{\omega }}^{*}=$Argument

(c) Solve the expression obtained in part (a) to obtain ${\mathrm{\omega }}_{\mathrm{i}}$ in terms of $\left\{\mathrm{i},\mathrm{\upsilon },\mathrm{and} \mathrm{r}\right\}$ .  ${\mathrm{\omega }}_{\mathrm{i}}=$

(d) If instead of a pair of spheres, we have two pairs of spheres as shown in figure below. What would be the new constant angular speed ${\mathrm{\omega }}^{*}$ of the assembly (i.e. the answer corresponding to part (b).