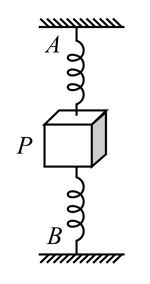
Two identical springs are attached to a small block $P$. The other ends of the springs are fixed at $A$ and $B$. When $P$ is in equilibrium the extension of top spring is $20 \mathrm{cm}$ and extension of bottom spring is $10 \mathrm{cm}$. The period of small vertical oscillations of $P$ about its equilibrium position is (use $g=9.8 \mathrm{m} {\mathrm{s}}^{-2}$).

        

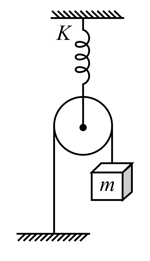
The below figure shows a system consisting of a massless pulley, a spring of force constant $k$ and a block of mass $m$. If the block is slightly displaced vertically downward from its equilibrium position and then released, the period of its vertical oscillation is

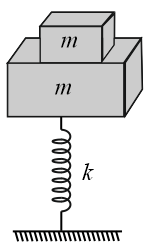
A block of mass $m$ is at rest on another block of the same mass as shown in the figure. Lower block is attached to a spring, the maximum amplitude of motion so that both the block will remain in contact is:

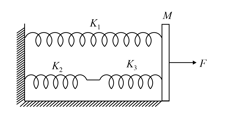
The springs shown in the figure are all up stretched in the beginning when a man starts pulling the block. The man exerts a constant force $F$ on the block.

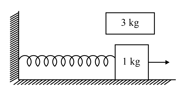
A $1 \mathrm{kg}$ block is executing simple harmonic motion of amplitude $0.1 \mathrm{m}$ on a smooth horizontal surface under the restoring force of a spring of spring constant $100 \mathrm{N} \mathrm{m}$. A block of mass $3 \mathrm{kg}$ is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, then

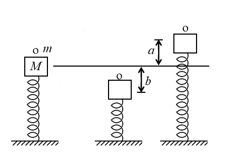
A mass $M$ is in static equilibrium on a massless vertical spring, as shown in the figure. A ball of mass $m$ dropped from certain height sticks to the mass $M$ after colliding with it. The oscillations they perform, reach to height $a$ above the original level of scales and depth $b$ below it.

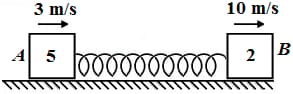
Two blocks $A (5 \mathrm{kg})$ and $B \left(2 \mathrm{kg}\right)$ attached to the ends of a spring constant $1120 \mathrm{N} {\mathrm{m}}^{-1}$ are placed on a smooth horizontal plane with the spring undeformed. Simultaneous velocities of $3 \mathrm{m} {\mathrm{s}}^{-1}$ and $10 \mathrm{m} {\mathrm{s}}^{-1}$ along the line of the spring in the same direction are imparted to $A$ and $B$ then