EASY
Earn 100
Two insulated circular loop and radius carrying a current of in the anti clockwise direction as shown in figure. The magnitude of the magnetic induction at the centre will be :
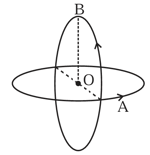

(a)
(b)
(c)
(d)
85.28% studentsanswered this correctly
Important Questions on Moving Charges and Magnetism
EASY
A current flows through a loop as shown in figure. The magnetic field at the Centre is
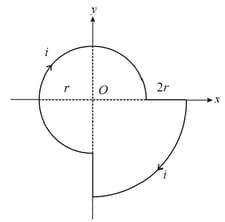
HARD
A small circular loop of conducting wire has radius a and carries current It is placed in a uniform magnetic field perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period The mass of the loop is then:
EASY
The magnetic field at the centre of a circular coil of turns and radius carrying a current of in tesla is
MEDIUM
Let is the magnetic field at the centre of the current carrying coil of radius and is the magnetic field on the axis of same circular coil at the distance of Then the ratio is
MEDIUM
Two infinitely long wires each carrying current along the same direction are made into the geometry as shown in the figure below.
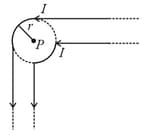
The magnetic field at the point is
MEDIUM
The coefficient of self-induction of a closely wound coil of turns and area of cross-section is . Find the magnetic induction at the centre of its core when a current of flows in it.
EASY
The magnetic field at the centre in the given figure is
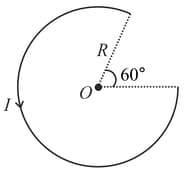
HARD
A circular coil connected to a battery of emf produced a certain magnetic induction field at its centre. The coil is unwound, stretched to double its length rewound into a coil of of the original radius and connected to a battery of emf to produce same field at the centre. Then is
EASY
Fill in the blank with the most appropriate option given below.
We should give everyone training in citizenship, but we have______this aspect till now.
EASY
The magnitude of a magnetic field at the centre of a circular coil of radius , having turns and carrying a current can be doubled by changing
MEDIUM
Two circular loops and of wire carrying equal and opposite currents are placed parallel to each other with a common axis. The radius of loop is and that of is . The distance between the centres of the loops is . The magnetic field at the centre of shall be zero if
EASY
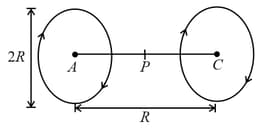
A Helmholtz coil has a pair of loops, each with turns and radius . They are placed coaxially at distance and the same current flows through the loops in the same direction. The magnitude of the magnetic field at midway between the centres and is given by [Refer to figure given below]:
EASY
A circular coil of radius carries an electric current . The magnetic field due to the coil at a point on the axis of the coil located at a distance from the centre of the coil, such that the magnetic field at that point is proportional to
MEDIUM
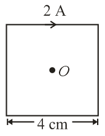
The magnetic field at the centre of the current-carrying square loop shown in the figure is
EASY
Magnetic field at the centre of a circular loop of area is . The magnetic moment of the loop will be ( permeability of free space)
HARD
A light charged particle is revolving in a circle of radius in electrostatic attraction of a static heavy particle with opposite charge. How does the magnetic field at the centre of the circle due to the moving charge depend on ?
MEDIUM
A circular loop of radius of conducting wire connected with a voltage source of zero internal resistance produces a magnetic field at its centre. If instead, a circular loop of radius , made of same material, having the same cross-section is connected to the same voltage source, what will be the magnetic field at its centre?
MEDIUM
A thin ring of radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of about its axis, perpendicular to its plane. Is the magnetic field its centre is , then the charge carried by the ring is close to
EASY
An electron moving in a circular orbit of radius makes rotations per second. The magnetic field produced at the center has magnitude:
MEDIUM
A circular coil carrying current has a radius and magnetic field at the centre is . The distance from the centre along the axis of the same coil where the magnetic field will be is

